ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 3 Rational Numbers Objective Type Questions
Mental Maths
Question 1.
Fill in the blanks:
(i) Two rational numbers are called equivalent if they have …… value.
(ii) The number \(\frac { -4 }{ 7 }\) lies to the …….. of zero on the number line.
(iii) The rational number \(\frac { -5 }{ -11 }\) lies to the ……. of zero on the number line.
(iv) The rational number \(\frac { -84 }{ 156 }\) reduced to simplest form is ………
(v) The standard form of the rational number \(\frac { 14 }{ -12 }\) is ………
(vi) There are ….. rational numbers between two different rational numbers.
(vii) Two rational numbers \(\frac { p }{ q }\)and \(\frac { r }{ s }\) are equal if an only if q × r = ……..
(viii)The multiplicative inverse of -3\(\frac { 1 }{ 5 }\) is ……..
(ix) \(\frac { -3 }{ 7 }\) ÷ \(\frac { -7 }{ 3 }\) = ………
(x) If p and q are positive integers, then \(\frac { p }{ q }\) is a …… rational number and \(\frac { p }{ -q }\) is a ……
Solution:
(i) Two rational numbers are called equivalent if they have same value.
(ii) The number \(\frac { -4 }{ 7 }\) lies to the left of zero on the number line.
(iii) The rational number \(\frac { -5 }{ -11 }\) or \(\frac { 5 }{ 11 }\) lies to the right of zero on the number line.
(iv) The rational number \(\frac { -84 }{ 156 }\) reduced to simplest form is \(\frac { -7 }{ 13 }\).
(v) The standard form of the rational number \(\frac { 14 }{ -12 }\) is \(\frac { -7 }{ 6 }\)
(vi) There are infinitely many rational numbers between two different rational numbers.
(vii) Two rational numbers \(\frac { p }{ q }\) and \(\frac { r }{ s }\) are equal if an only if q × r = p × s.
(viii)The multiplicative inverse of -3\(\frac { 1 }{ 5 }\) is \(\frac { -5 }{ 16 }\).
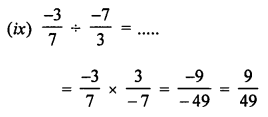
(x) If p and q are positive integers, then \(\frac { p }{ q }\) is a positive rational number and \(\frac { p }{ -q }\) is a negative rational number.
Question 2.
State whether the following statements are true (T) or false (F).
(i) Zero is the smallest rational number.
(ii) Every integer is a rational number.
(iii) Every rational number is an integer.
(iv) Every fraction is a rational number.
(v) Every rational number is a fraction.
(vi) The reciprocal of -1 is -1.
(vii) The quotient of two integers is always a rational number.
(viii) The value of a rational number remains the same if both its numerator and denominator are multiplied (or divided) by the same (nonzero) integer.
(ix) Between two distinct integers, we can always insert an integer.
(x) Between two distinct rational numbers, we can al ways insert a rational number.
(xi) There exists atleast one integer between two different rational numbers.
(xii) The reciprocal of 2\(\frac { 6 }{ 7 }\) is \(\frac { -7}{ 20 }\).
(xiii) All terminating decimal numbers are rational numbers.
Solution:
(i) Zero is the smallest rational number. (False)
Correct:
(∵ There is no end of smallest rational numbers)
(ii) Every integer is a rational number. (True)
(iii) Every rational number is an integer. (False)
Correct:
Every rational number is not an integer.
(iv) Every fraction is a rational number. (True)
(v) Every rational number is a fraction. (False)
(vi) The reciprocal of-1 is -1. (True)
(vii) The quotient of two integers is always a rational number. (False)
(viii)The value of a rational number remains the same if both is numerator and denominator are multiplied (or divided) by the same (non-zero) integer. (True)
(ix) Between two distinct integers, we can always insert an integer. (False)
Correct:
Between two integers, we can insert rational numbers.
(x) Between two distinct rational numbers, we can always insert a rational number. (True)
(xi) There exists atleast one integer between two different rational numbers. (False)
Correct:
It is not necessary that one integer will exist between two different rational numbers.
(xii) The reciprocal of 2\(\frac { 6 }{ 7 }\) is \(\frac { -7 }{ 20 }\). (False)
Correct:
The reciprocal of 2\(\frac { 6 }{ 7 }\) or \(\frac { 20 }{ 7 }\) is \(\frac { 7 }{ 20 }\) not \(\frac { -7 }{ 20 }\).
(xiii) All terminating decimal numbers are rational numbers. (True)
Multiple Choice Questions
Choose the correct answer from the given four options (3 to 14):
Question 3.
The rational number \(\frac { 110 }{ -132 }\) when reduced to standard form is
(a) \(\frac { 10 }{ -12 }\)
(b) \(\frac { 5 }{ -6 }\)
(c) \(\frac { -5 }{ 6 }\)
(d) \(\frac { 110 }{ -132 }\)
Solution:
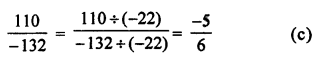
Question 4.
The Additive inverse of \(\frac { -7 }{ 12 }\) is
(a) \(\frac { 12 }{ -7 }\)
(b) \(\frac { -7 }{ 12 }\)
(c) \(\frac { -5 }{ 12 }\)
(d) \(\frac { 7 }{ 12 }\)
Solution:
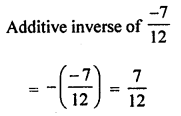
Question 5.
The Multiplicative inverse of \(\frac { -4 }{ 9 }\) is
(a) \(\frac { 4 }{ 9 }\)
(b) \(\frac { -9 }{ 4 }\)
(c) \(\frac { 9 }{ 4 }\)
(d) none of these
Solution:
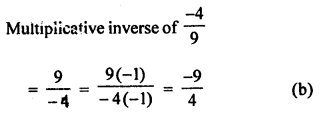
Question 6.
The reciprocal of the rational number -2\(\frac { 3 }{ 7 }\) is
(a) \(\frac { -17 }{ 7 }\)
(b) \(\frac { 7 }{ 17 }\)
(c) \(\frac { -7 }{ 17 }\)
(d) none of these
Solution:
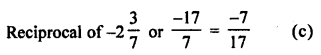
Question 7.
The product of rational number \(\frac { -2 }{ 5 }\) and its multiplicative inverse is
(a) 1
(b) 0
(c) \(\frac { 4 }{ 25 }\)
(d) \(\frac { 2 }{ 5 }\)
Solution:

Question 8.
The product of rational number \(\frac { -2 }{ 3 }\) and its additive inverse is
(a) 1
(b) \(\frac { 2 }{ 3 }\)
(c) \(\frac { 4 }{ 9 }\)
(d) \(\frac { -4 }{ 9 }\)
Solution:
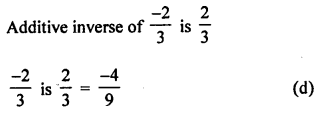
Question 9.
The sum of rational number \(\frac { -1 }{ 3 }\) and its reciprocal is
(a) 0
(b) 1
(c) \(\frac { -10 }{ 3 }\)
(d) \(\frac { -3 }{ 10 }\)
Solution:
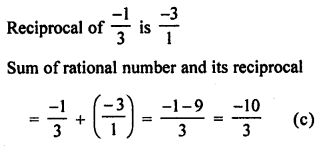
Question 10.
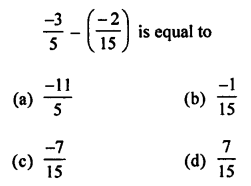
Solution:
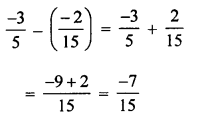
Question 11.
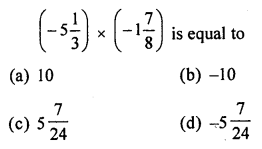
Solution:
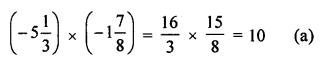
Question 12.
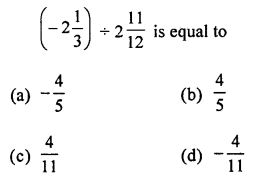
Solution:
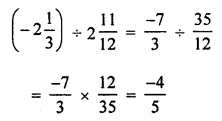
Question 13.
In the standard form of a rational number, the denominator is always
(a) 0
(b) a negative integer
(c) 1
(d) a positive integer
Solution:
In a standard form of a rational number, the denominator is always a positive integer. (d)
Question 14.
The sum of two rational numbers is -1. If one of them is \(\frac { -5 }{ 7 }\), then the other is
(a) \(\frac { 5 }{ 7 }\)
(b) \(\frac { -2 }{ 7 }\)
(c) \(\frac { 12 }{ 7 }\)
(d) \(\frac { -12 }{ 7 }\)
Solution:
The sum of two rational number is -1
One of them = \(\frac { -5 }{ 7 }\)
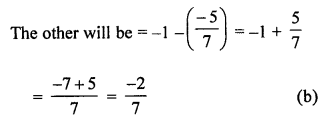
Value Based Questions
Question 1.
Rohit donated \(\frac { 1 }{ 5 }\) of his monthly income to an NGO working for the education of old women, \(\frac { 1 }{ 4 }\) of his salary spent on food, \(\frac { 1 }{ 3 }\) on rent and \(\frac { 1 }{ 15 }\) on other expenses. If he is left with ₹ 9000, find his monthly income. What values are being promoted?
Solution:
Let salary = ₹ 1

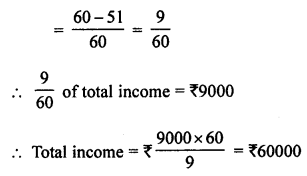
His donation to NGO who is working for the education of the old women is remarkable.
Higher Order Thinking Skills (HOTS)
Question 1.
From a rope 15 m long, 4\(\frac { 1 }{ 3 }\) m is cut off and \(\frac { 3 }{ 5 }\) of the remaining is cut off again. Find the length of the remaining part of the rope.
Solution:
Length of a rope = 15 m

Question 2.
Perimeter of a rectangle is 2 m less than \(\frac { 2 }{ 5 }\) of the perimeter of a square, if the perimeter of the square is 40 m, find the length and breadth of the rectangle given that the breadth is \(\frac { 1 }{ 3 }\) of the length.
Solution:
Perimeter of a square = 40 m
Perimeter of rectangle = \(\frac { 2 }{ 5 }\) of 40 – 2 = 16 – 2 = 14 m
Perimeter of rectangle = 2(Length + Breadth)
