ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 17 Data Handling Check Your Progress
Question 1.
State whether the following statement is true or false. Justify your answer:
“The median is always one of the numbers in data.”
Solution:
False.
As median of observations can depend on its odd number or even number.
In case of even observations, it will be the mean of two middle observation.
Question 2.
Marks obtained by five students of class VII in quarterly and half-yearly examination in Mathematics (out of 25) are given below:
| Students | Ashish | Arun | Kavish | Maya | Rita |
| Quarterly | 10 | 15 | 12 | 21 | 9 |
| Half-Yearly | 15 | 18 | 16 | 20 | 15 |
Represent the above data by a bar graph and answer the following questions:
(i) Do you see any improvement? Justify your answer.
(ii) Who has not done better?
Solution:
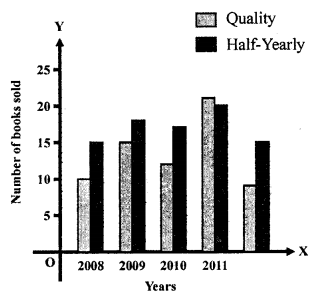
(i) Yes, we see that all bars representing half-yearly
marks are higher in all cases except one in Maya’s case.
So, there is an improvement.
(ii) Maya has not done better.
Question 3.
Find the mean of the factors of 12.
Solution:
Factors of 12
1, 2, 3, 4, 6, 12
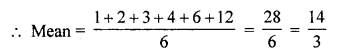
Question 4.
Find the median and the mode of the following data:
2, 14, 16, 12, 13, 14, 16, 13, 10, 14, 18, 9
Solution:
Arranging in ascending order:
2, 9, 10, 12, 13, 13, 14, 14, 14, 16, 16, 18
Here n = 12 which is even
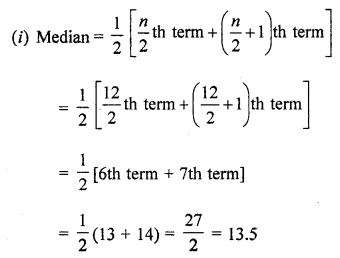
Mode: Observation 14 came the highest time.
Mode = 14
Question 5.
Heights (in cm) of 25 students are given below:
168, 165, 163, 160, 163, 161, 162, 164, 163, 162, 164, 163, 160, 163, 157, 165, 148, 163, 164, 160, 165, 163, 152, 155, 163.
What is the mode of their heights?
Solution:
Arranging in ascending order:
148, 152, 155, 157, 160, 160, 160, 161, 162, 162, 163, 163,
163, 163, 163, 163, 163, 163, 164, 164, 164, 165, 165, 168
We see that 163 comes maximum times
Mode = 163
Question 6.
A die is thrown, what is the probability of getting an odd prime number?
Solution:
A die is thrown,
Probability of odd prime number are 3, 5
Now, total outcomes = 6
and favourable outcomes = 2
Probability = \(\frac { 2 }{ 6 }\) = \(\frac { 1 }{ 3 }\)
Question 7.
A letter is chosen at random from the letters of the word MATHEMATICS, what is the probability of getting
(i) letter M
(ii) a vowel
(iii) a consonant?
Solution:
Word: MATHEMATICS
Total number of letters = 11
(i) Probability of getting M = \(\frac { 2 }{ 11 }\)
(ii) Probability of a vowel (n) = \(\frac { 4 }{ 11 }\)
(iii) Probability of getting a consonant (11 – 4 = 7) = \(\frac { 7 }{ 11 }\)