ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 14 Symmetry Ex 14.2
Question 1.
Which of the following figures have rotational symmetry? In case of rotational symmetry, find the order of rotational symmetry.
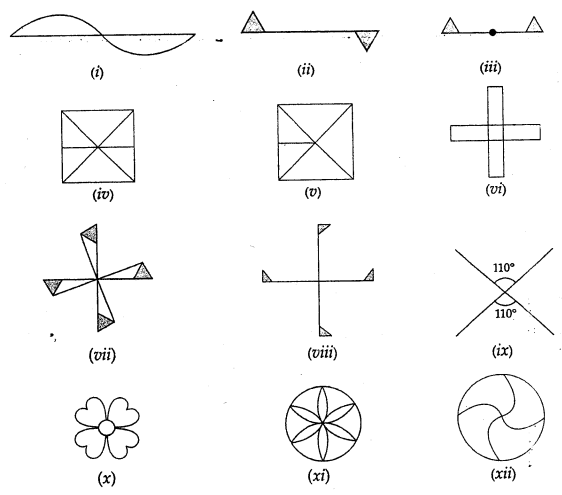
Solution:
(i) In figure (i) the rotational symmetry is of order is 2.
(ii) In figure (ii) the rotational symmetry is of order 2.
(iii) In figure (iii) there is no rotational symmetry.
(iv) In figure (iv) the rotational symmetry is of order 2.
(v) In figure (v) there is no rotational symmetry.
(vi) In figure (vi) there is rotational symmetry of order 4.
(vii) In figure (vii) there is rotational symmetry of order 1.
(viii)In figure (viii) there is no rotational symmetry.
(ix) In figure (ix) there is rotational symmetry of order 2.
(x) In figure (x) there is rotational symmetry of order 4.
(xi) In figure (xi) there is rotational symmetry of order 6.
(xii) In figure (xii) there is rotational symmetry of order 4.
Question 2.
Which of the following figures have rotational symmetry of order greater than 1?
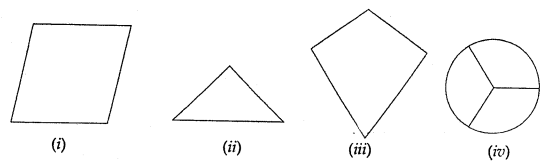
Solution:
From the given figure,
Figure (i) and (iv) i.e., rhombus and circle have
rotational symmetry more than order 1.
A rhombus has 2 and a circle has many.
Question 3.
Name any two figures that have both lines of symmetry and rotational symmetry.
Solution:
Rhombus and an equilateral triangle have
both line of symmetry and rotational symmetry.
Question 4.
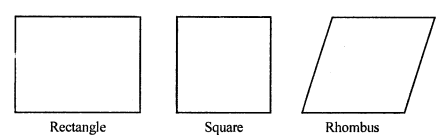
Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
Solution:
In a quadrilateral, rectangle, square and rhombus have both line of symmetry
as well as rotational symmetry.
Question 5.
Draw a rough sketch of:
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only one line of symmetry and no rotational symmetry of order more than 1.
(iii) a triangle with no line symmetry but rotational symmetry of order 1.
(iv) a quadrilateral with no line symmetry but rotational symmetry of order more than 1.
(v) a quadrilateral with line symmetry but not rotational symmetry of order more than 1.
Solution:
(i) A triangle with both line and
rotational symmetry of order more than 1.
It is an equilateral triangle.
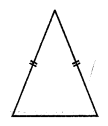
(ii) A triangle with only one line of symmetry
but no rotational symmetry of order more than 1.
It is an isosceles triangle.
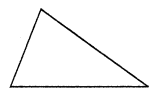
(iii) A triangle having no line symmetry
but rotational symmetry of order 1.
It is a scalene triangle.
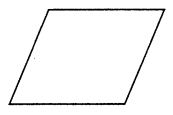
(iv) A quadrilateral with no line symmetry
but rotational symmetry of order more than 1.
It is a parallelogram.
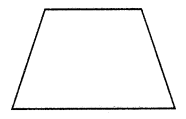
(v) A quadrilateral, with the line of symmetry
but not rotational symmetry of order more than 1.
It is an isosceles trapezium.
Question 6.
If a figure has two or more than two lines of symmetry, can it have rotational symmetry of order more than one?
Solution:
If it has two or more lines of symmetry, then,
yes, it can have rotational symmetry of order more than one.
A circle is its example.
Question 7.
A figure looks exactly the same as its original figure after rotation of 60°. At what other angles will this figure appear the same?
What can you say if the angle of rotation is
(i) 72°
(ii) 45°
(iii) 50°?
Solution:
A figure looks exactly the same as its original after rotation of 60°.
It will also like the same after rotation of 120°, 180°, 240°, 300°, and 360°.
(i) If the angle of rotation of symmetry is 72°
then it will look exactly the same after it rotates after 144°, 216°, 288°, 360°.
(ii) If the angle of rotation of symmetry is 45°,
then it will look exactly the same after 90°, 135°, 180°, 225°, 270°, 315°, and 360°.
(iii) If the angle of rotation is 50°, then it is not possible.
Question 8.
Can a figure possessing rotational symmetry have an angle of rotation of measure
(i) 180°
(ii) 120°
(iii) 90°
(iv) 30°
(v) 15°
(vi) 17°?
Solution:
(i) 180° : Yes, it can have as \(\frac { 360 }{ 180 }\) = 2°
(ii) 120° : Yes, it can have as \(\frac { 360 }{ 120 }\) = 3°
(iii) 90° : Yes, it can have as \(\frac { 360 }{ 90 }\) = 4°
(iv) 30° : Yes, it can have as \(\frac { 360 }{ 30 }\) = 12°
(v) 15° : Yes, it can have as \(\frac { 360 }{ 15 }\)= 24°
(vi) 17° : No, it cannot have as \(\frac { 360 }{ 17 }\) is not exactly divisible.