ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 11 Triangles and its Properties Ex 11.5
Question 1.
PQR is a triangle, right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Solution:
In ΔPQR, ∠P = 90°
PQ = 10 cm, PR = 24 cm
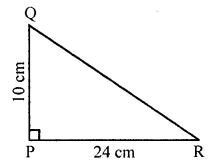
Using Pythagoras Theorem,
QR2 = PQ2 + PR2 = 102 + 242 = 100 + 576 = 676 = (26)2
QR = 26 cm
Question 2.
ABC is a triangle, right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Solution:
In ΔABC, ∠C = 90°
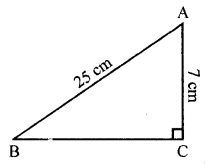
AB = 25 cm and AC = 7 cm
AB2 = AC2 + BC2
⇒ (25)2 = (7)2 + BC2
⇒ 625 = 49 + BC2
⇒ BC2 = 625 – 49 = 576 = (24)2
⇒ BC = 24 cm
Question 3.
Find the value of x in each of the following figures. All measurements are in centimeters.
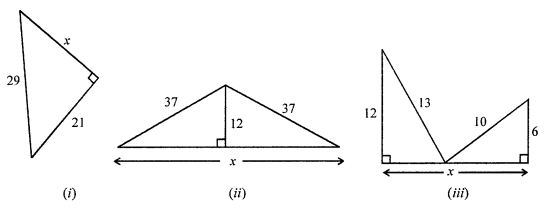
Solution:
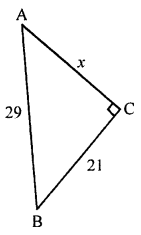
(i) In ΔABC, ∠C = 90°
AB = 29, BC = 21, AC = x
AB2 = AC2 + BC2 (Using Pythagoras theorem)
⇒ (29)2 = (21)2 + x2
⇒ 841 = 441 + x2
⇒ x2 = 841 – 441 = 400 = (20)2
x = 20
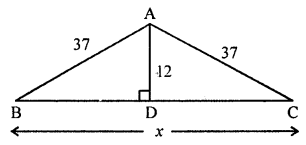
(ii) In ΔABC, AD ⊥ BC
AB = 37, AC = 37
In right ΔABD
AB2 = AD2 + BD2 (Pythagoras Theorem)
⇒ (37)2 = (12)2 + BD2
⇒ 1369 = 144 + BD2
⇒ BD2 = 1369 – 144
⇒ BD2 = 1225 = (35)2
⇒ BD = 35 cm
But AD bisects BC at D
BC = 2 × BD
⇒ x = 2 × 35 = 70 cm
(iii) In right ΔABE, ∠B = 90°
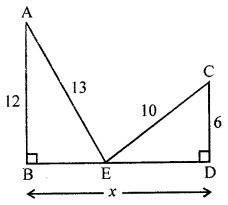
AE2 = AB2 + BE2 (Pythagoras Theorem)
⇒ (13)2 = 122 + BE2
⇒ 169 = 144 + BE2
⇒ BE2 = 169 – 144 = 25 = (5)2
⇒ BE = 5 cm
Similarly in right ΔCDE, ∠D = 90°
CE2 = CD2 + ED2
⇒ 102 = 62 + ED2
⇒ 100 = 36 + ED2
⇒ ED2 = 100 – 36 = 64 = (8)2
⇒ ED = 8 cm
Now, BD = x = BE + ED = 5 + 8 = 13 cm
Question 4.
Which of the following can be the sides of a right angled triangle?
(i) 4 cm, 5 cm, 7 cm
(ii) 1.5 cm, 2 cm, 2.5 cm
(iii) 7 cm, 5.6 cm, 4.2 cm
Solution:
(i) Sides are : 4 cm, 5 cm, 7 cm
(Longest side)2 = (7)2 = 49
Sum of squares of other two sides
= 42 + 52
= 16 + 25
= 41
49 ≠ 41
These are not the sides of the right triangle.
(ii) Sides are : 1.5 cm, 2 cm, 2.5 cm
(Longest side)2 = (2.5)2 = 6.25
Sum of the squares of the other two sides
= 1.52 + 22
= 2.25 + 4
= 6.25
6.25 = 6.25
There are the sides of a right triangle
and right angle is opposite to the side 2.5 cm
(iii) Sides are : 7 cm, 5.6 cm, 4.2 cm
(Longest side)2 = 72 = 49
Sum of the squares of the other two sides
= (5.6)2 + (4.2)2
= 31.36 + 17.64
= 49
49 = 49
These are the sides of a right triangle
Right angle is opposite to the side 5.6 cm
Question 5.
A 15 m long ladder reaches a window 12 m high from the ground on placing it against a wall. How far is the foot of the ladder from the wall?
Solution:
Let length of ladder AB = 15 m
and height of wind AC = 12 m
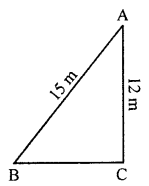
BC is the distance from wall to the foot of ladder
In right ΔABC, ∠C = 90°
AB2 = AC2 + BC2 (Pythagoras Theorem)
⇒ (15)2 = 122 + BC2
⇒ 225 = 144 + BC2
⇒ BC2 = 225 – 144 = 81 = (9)2
⇒ BC = 9 m
Distance of the foot of the ladder and the wall = 9 m
Question 6.
Find the area and the perimeter of the rectangle whose length is 15 cm and the length of one diagonal is 17 cm.
Solution:
Length of a rectangle = 15 cm
and length of its one diagonal = 17 cm
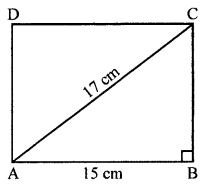
In right ΔABC
AC2 = AB2 + BC2 (Pythagoras Theorem)
⇒ 172 = 152 + BC2
⇒ 289 = 225 + BC2
⇒ BC2 = 289 – 225 = 64 = (8)2
Breadth = 8 cm
Area = Length × Breadth = 15 × 8 = 120 cm2
and perimeter = 2(Length + Breadth)
= 2(15 + 8)
= 2 × 23
= 46 cm
Question 7.
If the diagonals of a rhombus measure 10 cm and 24 cm, find its perimeter.
Solution:
Length of diagonals of a rhombus are 10 cm and 24 cm
The diagonals of a rhombus bisect each other at right angles.
O is the mid-point of AC and BD
AO = OC = \(\frac { 24 }{ 2 }\) = 12 cm
and BO = OD = \(\frac { 10 }{ 2 }\) = 5 cm
Now in right ΔAOB
AB2 = AO2 + BO2 (Pythagoras Theorem)
⇒ AB2 = 122 + 52
⇒ AB2 = 144 + 25 = 169 = (13)2
⇒ AB = 13 cm
Perimeter of rhombus = 4 × Side = 4 × 13 = 52 cm
Question 8.
The side of a rhombus is 5 cm. If the length of one diagonal of the rhombus is 8 cm, then find the length of the other diagonal.
Solution:
Side of a rhombus = 5 cm
Length of one diagonal (AC) = 8 cm
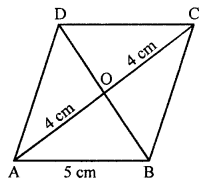
The diagonal of a rhombus bisect
each other at right angles.
AO = OC = 4 cm, BO = OD
In right ΔAOB,
AB2 = AO2 + BO2
52 = 42 + BO2
25 = 16 + BO2
BO2 = 25 – 16 = 9 = (3)2
BO = 3 cm
and diagonal BD = 2 × 3 = 6 cm