ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 11 Triangles and its Properties Ex 11.2
Question 1.
Find the value of the unknown exterior angle x in each of the following diagrams:
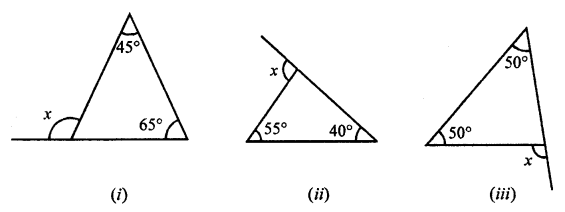
Solution:
We know that the exterior angle of a triangle
is equal to the sum of its interior opposite angles.
Therefore,
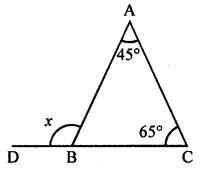
(i) Ext. ∠x = 45° + 65° = 110°
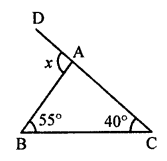
(ii) Ext. ∠x = 55° + 40° = 95°
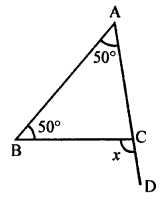
(iii) Ext. ∠x = 50° + 50° = 100°
Question 2.
Find the value of the unknown interior angle x in each of the following diagrams:
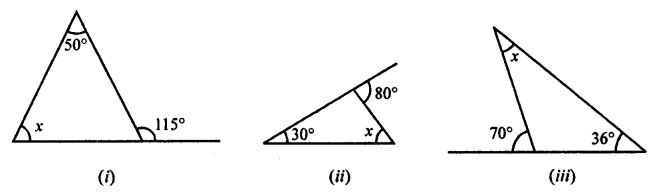
Solution:
We know that the exterior angle of a triangle
is equal to the sum of its interior opposite angles.
Therefore,
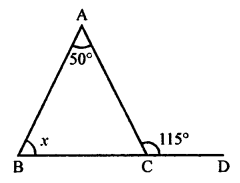
(i) In the given triangle,
Ext. ∠115° = x + 50°
⇒ x = 115° – 50° = 65°
⇒ x = 65°
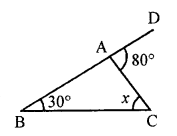
(ii) In given triangle,
Ext. ∠80° = 30° + x
⇒ x = 80° – 30° = 50°
⇒ x = 50°
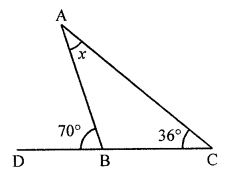
(iii) In given triangle,
Ext. ∠70° = x + 36°
⇒ x = 70° – 36° = 34°
⇒ x = 34°
Question 3.
Find the value of x in each of the following diagrams:
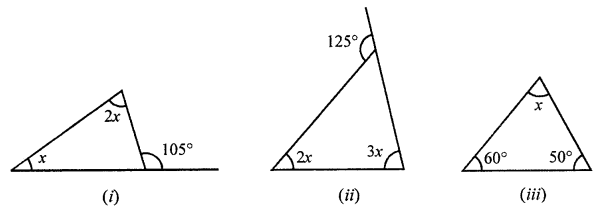
Solution:
We know that the exterior angle of a triangle
is equal to the sum of its interior opposite angles.
Therefore,
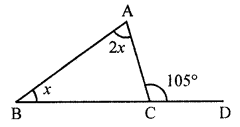
(i) In a given triangle,
Ext. ∠105° = 2x + x
⇒ 3x = 105°
⇒ x = 35°
x = 35°
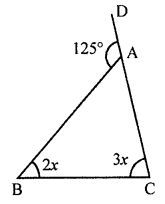
(ii) In given triangle,
Ext. ∠125° = 2x + 3x
⇒ 5x = 125°
⇒ x = 25°
x = 25°
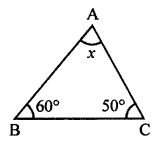
(iii) In given triangle,
∠A + ∠B + ∠C = 180°
(Sum of angles of a triangle)
⇒ x + 60° + 50° = 180°
⇒ x + 110° = 180°
⇒ x = 180° – 110° = 70°
x = 70°
Question 4.
Find the value of unknown x in each of the following:
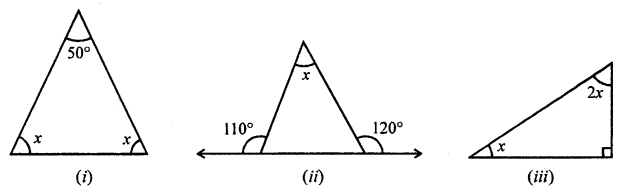
Solution:
(i) In given triangle = Let ∆ABC
∠A + ∠B + ∠C = 180°
⇒ 50° + x + x = 180°
⇒ 2x = 180° – 50° = 130°
Hence, x = 65°
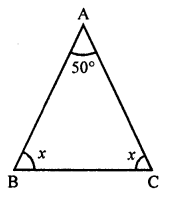
(ii) In the given figure,
Let the name of ∆ be ABC
∠ABC + ∠ABE = 180°
⇒ ∠ABC + 110° = 180°
⇒ ∠ABC = 180° – 110° = 70°
Similarly,
∠ACB + ∠ACD = 180°
⇒ ∠ACB + 120° = 180°
⇒ ∠ACB = 180° – 120° = 60°
Now in ∆ABC
∠BAC + ∠ABC + ∠ACB = 180°
⇒ x + 70° + 60° = 180°
⇒ x + 130° = 180°
⇒ x= 180° – 130° = 50°
⇒ x = 50°
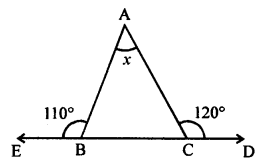
(iii) Let the given triangle be named as ∆ABC,
where ∠C = 90°
In ∆ABC,
∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ 2x + x + 90° = 180°
⇒ 3x = 180° – 90° = 90°
⇒ x = 30°
Question 5.
Find the values of x and y in each of the following diagrams:
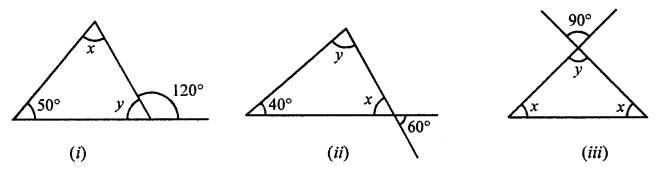
Solution:
We know that an exterior angle of a triangle
is equal to the sum of its interior opposite angle.
Therefore,
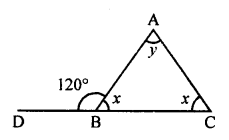
(i) Let the ∆’s name = ∆ABC
In ∆ABC
Ext. ∠ACD = ∠A + ∠B
120° = x + 50°
⇒ x = 120° – 50° = 70°
But ∠ACD + ∠ABC = 180° (Linear pair)
120° + y = 180°
⇒ y = 180° – 120° = 60°
x = 70°, y = 60°
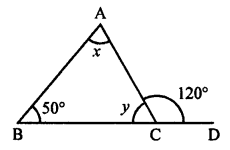
(ii) In the given figure,
∠ACB = ∠DCE (Vertically opposite angles)
x = 60°
But ∠A + ∠B + ∠ACB = 180°
(Sum of angles of a triangle)
⇒ y + 40° + x = 180°
⇒ y + 40° + 60° = 180°
⇒ y + 100° = 180
⇒ y = 180° – 100° = 80°
Hence, x = 60°, y = 80°
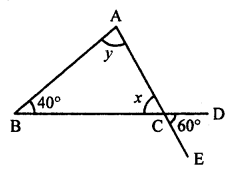
(iii) In the given figure,
∠BAC = ∠EAF (Vertically opposite angles)
y = 90°
In ∆ABC,
∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ y + x + x = 180°
⇒ 90° + 2x = 180°
⇒ 2x = 180° – 90° = 90°
⇒ x = 45°
Hence, x = 45°
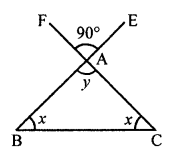
Question 6.
Find the values of x and y in each of the following diagrams:
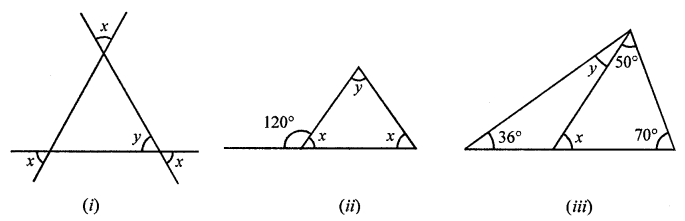
Solution:
(i) In the given figure,
In ∆ABC,
x = y (Vertically opposite angles)
Similarly,
∠BAC = y, ∠ABC = y, ∠BCA = y
But ∠BAC + ∠ABC + ∠BCA = 180°
(Angles of a triangle)
⇒ y + y + y = 180°
⇒ 3y = 180°
⇒ y = 60°
x = 60°, y = 60°
(ii) In ∆ABC,
∠ABC + ∠ABD = 180°
⇒ x + 125° = 180°
⇒ x = 180°- 125° = 55°
and Ext. ∠ABD = x + y
⇒ 125° = 55° + y
⇒ y = 125° – 55° = 70°
x = 55°, y = 70°
(iii) In ∆ABC,
Ext. ∠ABD = ∠A + ∠B = 50° + 70° = 120°
But ∠ABC + ∠ABD = 180° (Linear pair)
⇒ x + ∠ABD = 180°
⇒ x + 120° = 180°
⇒ x = 180° – 120° = 60°
But in ∆ABD
Ext. ∠ABC = ∠D + ∠DAB
⇒ x = y + 30°
⇒ 60° = y + 30°
⇒ y = 60° – 30° = 30°
x = 60°, y = 30°
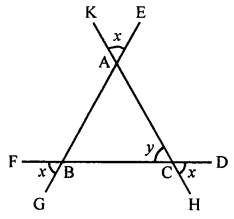
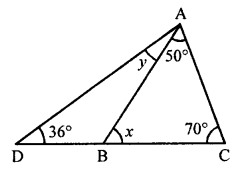
Question 7.
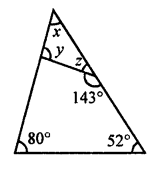
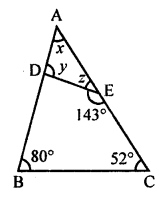
In the adjoining figure, find the size of each lettefed angle.
Solution:
In the given figure,
In ∆ABC
∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ x + 80° + 52° = 180°
⇒ x + 132° = 180°
⇒ x = 180° – 132° = 48°
∠DEC + ∠DEA = 180° (Linear pair)
⇒ 143° + z = 180°
⇒ z = 180° – 143° = 37°
Now in ∆ADE
Ext. ∠DEC = ∠A + ∠ADE
⇒ 143° = x + y
⇒ 143° = 48° + y
⇒ y = 143° – 48° = 95°
x = 48°, y = 95°, z = 37°
Question 8.
One of the angles of a triangle measures 80° and the other two angles are equal. Find the measure of each of the equal angles.
Solution:
One angle of an ∆ABC = 80°
Let ∠A = 80° and the other two angles are equal
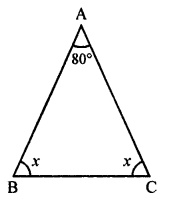
Let ∠B = ∠C = x
In ∆ABC,
∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ 80° + x + x = 180°
⇒ 2x = 180° – 80° = 100°
⇒ x = 50°
∠A = 80°, ∠B = 50°, ∠C = 50°
Question 9.
If one angle of a triangle is 60° and the other two angles are in the ratio 2 : 3, find these angles.
Solution:
One angle of a triangle = 60°
Other two angles are in the ratio 2 : 3
Sum of other two angles = 180° – 60° = 120°
Let one of other two angles = 2x
Then third angle = 3x
2x + 3x = 120°
⇒ 5x = 120°
⇒ x = 24
Other two angles are 2x = 2 × 24 = 48°
and 3x = 3 × 24 = 72°
Other two angles of the triangle are 48°, 72°
Question 10.
If the angles of a triangle are in the ratio 1 : 2 : 3, find the angles. Classify the triangle in two different ways.
Solution:
Sum of angles of a triangle = 180°
Ratio in the angles of a triangle = 1 : 2 : 3
Let first angle = x
Second angle = 2x
Third angle = 3x
x + 2x + 3x = 180°
⇒ 6x = 180°
⇒ x = 30°
∴ First angle = 30°
Second angle = 30° × 2 = 60°
and third angle = 30° × 3 = 90°
∵ One angles is 90°
∴ It is a right angled triangle
∵ Sides an different
∴ It is a scalene triangle.
Question 11.
Can a triangle have three angles whose measures are
(i) 65°, 74°, 39°?
(ii) \(\frac { 1 }{ 3 }\) right angle, 1 right angle, 60°?
Solution:
We know that sum of angles of a triangle = 180°
(i) Angles are 65°, 74°, 39°
Sum of angles = 65° + 74° + 39° = 178°
178° ≠ 180°
There three angles can not be of triangle
(ii) \(\frac { 1 }{ 3 }\) right angle = \(\frac { 1 }{ 2 }\) × 90° = 30°
1 right angle = 90°
Third angle = 60°
Sum of angles = 30° + 90° + 60° = 180°
These angles are of a triangle.