ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 11 Triangles and its Properties Check Your Progress

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 11 Triangles and its Properties Check Your Progress

Question 1.
Find the value of x in each of the following diagrams:

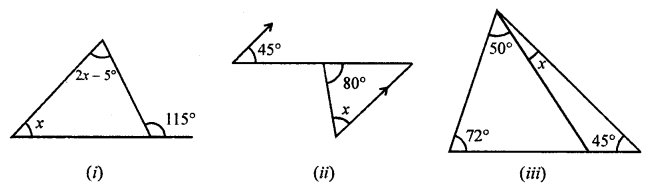
Solution:
(i) In the given figure,

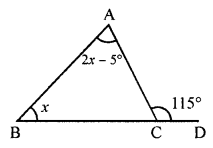
Ext. angle of triangle = Sum of its interior opposite angles.
⇒ 115° = 2x – 50 + x
⇒ 3x – 50 = 115°
⇒ 3x = 115° + 5° = 120°
⇒ x = 40°
x = 40°
(ii) In the given figure,

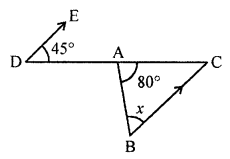
∠1 = 45° (Alternate angles)
Now in triangle,
80° + x + ∠1 = 180° (Sum of angles of a triangle)
⇒ 80°+ x + 45° = 180°
⇒ x + 125°= 180°
⇒ x = 180° – 125° = 55°
(iii) In ∆ABC
∠BAC + ∠ABC + ∠ACB = 180° (Sum of angles of a triangle)

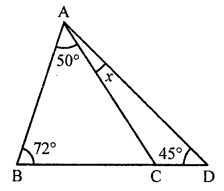
⇒ 50° + 72° + ∠ACB = 180°
⇒ 120° + ∠ACB = 180°
⇒ ∠ACB = 180°- 122° = 58°
Now in ∆ACD
Ext. ∠ACB = ∠CAB + ∠CDA
⇒ 58° = x + 45°
⇒ x = 58° – 45° = 13°

Question 2.
In the given figure, ∠B = 70° and ∠A = 50°. If the bisector of ∠C meets AB in D, then find ∠ADC.

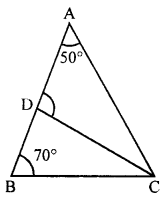
Solution:
In the given figure,
∠A = 50°, ∠B = 70°, ∠ADC = x
CD is the bisector of ∠C
In ∆ABC,
∠A + ∠B + ∠ACB = 180° (Angles of a triangle)
⇒ 50° + 70° + ∠ACB = 180°
⇒ 120° + ∠ACB = 180°
⇒ ∠ACB = 180°- 120° = 60°
But CD is the bisector of ∠C
∠DCB = \(\frac { 60 }{ 2 }\) = 30°
Now in ∆BCD,
Ext. ∠ADC = ∠B + ∠DCB (Interior opposite angles)
= 70° + 30° = 100°

Question 3.
Find the values of x and y in each of the following figures:

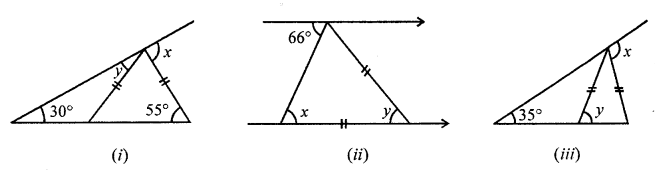
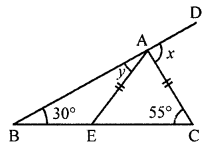
Solution:
(i) In the given figure, AC = AE
Ext. ∠DAC = ∠B + ∠C (Interior opposite angles)
⇒ x = 30° + 55° = 85°
In ∆AEC,
AC = AE
∠AEC = ∠ACE = 55°
In ∆ABE,
Now, Ext. ∠AEC = y + 30°
⇒ 55° = y + 30°
⇒ y = 55° – 30° = 25°
x = 85° and y = 25°

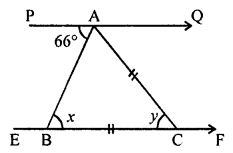
(ii) In the given figure,
PQ || EF
In ∆ABC,
AC = BC
∠PAB = 66°
∠ABC = ∠PAB (Alternate angles)
x = 66°
AC = BC
∠BAC = ∠ABC = 66°
But ∠ABC + ∠ACB + ∠BAC = 180° (Angles of a triangle)
⇒ 66°+ y + 66° = 180°
⇒ 132° + y = 180°
⇒ y = 180° – 132° = 48°
x = y = 48°

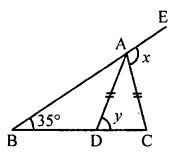
(iii) In the given figure,
BD = AD = AC
∠B = 35°
In ∆ABD
AD = BD
∠BAD = ∠ABD = 35°
Now, Ext. ∠ADC = B + BAD
y = 35° + 35° = 70°
In ∆ADC,
AD = AC
∠ACD = ∠ADC = y = 70°
and Ext. ∠EAC = ∠ABC + ∠ACB = 35° + 70° = 105°
Hence, x = 105°, y = 70°

Question 4.
If the two acute angles of a right-angled triangle are in the ratio 7 : 8, find these angles.
Solution:
In a right-angled triangle.
Sum of two acute angles = 90°
Ratio in two angles = 7 : 8
First angle = \(\frac { 90 }{ 7+8 }\) × 7
= \(\frac { 90 }{ 15 }\) × 7 = 42°
and second angle = \(\frac { 90 }{ 15 }\) × 8 = 48°

Question 5.
If the angles of a triangle are (3x)°, (2x – 7)° and (4x – 11)°, then find the value of x.
Solution:
Angles of a triangle are (3x)°, (2x – 7)° and (4x – 11)°
But sum of three angles of a triangle = 180°
3x + 2x – 7 + 4x – 11° = 180°
⇒ 9x – 18° = 180°
⇒ 9x = 180° + 18° = 198°
⇒ x = 22°

Question 6.
In an isosceles triangle, the vertical angle is 15° greater than each of its base angles. Find all the angles of the triangle.
Solution:
In an isosceles triangle,
Vertical angle = 15° greater than each base angles
Let each base angle = x
Then vertical angle = x + 15°
Now sum of angles of a triangle = 180°
x + 15° + x + x = 180°
⇒ 3x + 15° = 180°
⇒ 3x = 180° – 15° = 165°
⇒ x = 55°
Each base angle = 55°
and vertical angle = 55° + 15° = 70°

Question 7.
Can a triangle have three sides whose lengths are
(i) 4.5 cm, 3.8 cm, 7.2 cm?
(ii) 3.2 cm, 5.3 cm, 9.4 cm?
Solution:
(?) Sides are 4.5 cm, 3.8 cm, 7.2 cm
Sum of two sides = 4.5 + 3.8 = 8.3 cm
8.3 > 7.2 cm
The triangle can have there sides.
(ii) Sides are 3.2 cm, 5.3 cm, 9.4 cm
Sum of sides 3.2 and 5.3 cm = 3.2 + 5.3 = 8.5 cm
8.5 cm < 9.4 cm
The triangle does not have there sides.

Question 8.
If the lengths of two sides of a triangle are 5 cm and 12 cm, then what can be the length of the third side?
Solution:
Length of two sides of a triangle is 5 cm and 12 cm
Sum of there two sides = 5 + 12 = 17 cm
and difference = 12 – 5 = 7 cm
The third side will be greater than 7 cm but less than 17 cm.

Question 9.
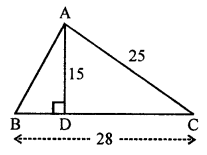
In the given figure, all measurements are in centimeters. If AD is perpendicular to BC, find the length of AB.

Solution:
In the given figure,
ABC is a triangle in which AC = 25 cm, BC = 28 cm
AD ⊥ BC and AD = 15 cm
To find the length of AB
In right ∆ADC
AC² = AD² + DC² (Pythagoras Theorem)
⇒ (25)² = 15² + DC²
⇒ 625 = 225 + DC²
⇒ DC² = 625 – 225 = 400 = (20)²
⇒ DC = 20 cm
But BC = 28 cm
BD = 28 – 20 = 8 cm
Now in right ∆ADB
AB² = AD² + BD²
= 15² + 8² = 225 + 64 = 289 = (17)²
⇒ AB = 17 cm

Question 10.
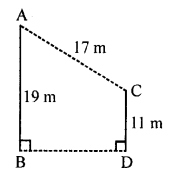
In the given figure, AB and CD are two vertical poles of height 19 m and 11 m respectively. If the shortest distance between their tops is 17 m, find how far apart they are?

Solution:
In the given figure,

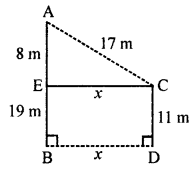
Pole AB = 19 m, Pole CD = 11 m
Distance between their tops AC = 17 cm
Draw EC || BD, then
Let BD = CE = x
EB = CD = 11 m
AE = AB – EB = 19 – 11 = 8m
Now in right ∆AEC,
AC² = AE² + EC²
⇒ (17)² = (8)² + x²
⇒ 289 = 64 + x²
⇒ x² = 289 – 64 = 225 = (15)²
⇒ x = 15
BD = EC = x = 15m

ML Aggarwal Class 7 Solutions for ICSE Maths