ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 14 Mensuration Check Your Progress
Question 1.
Look at the given figure and fill in the following blanks:
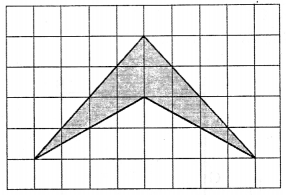
(i) The contribution in estimation of given area due to completely covered squares is
(ii) The contribution in estimation of given area due to more than half covered squares is
(iii) The contribution in estimation of given area due to exactly half covered square, is
(iv) The contribution in estimation of given area due to less than half covered squares is
(v) The total estimated area is
Solution:
(i) The contribution in estimation of given area
due to completely covered squares is 2 sq. units.
(ii) The contribution in estimation of given area
due to more than half covered squares is 2 sq. units.
(iii) The contribution in estimation of given area
due to exactly half covered square is 3 sq. units.
(iv) The contribution in estimation of given area
due to less than half covered squares is 0 sq. units.
(v) The total estimated area is 7 sq. units.
Question 2.
The perimeter of a square ABCD is twice the perimeter of ∆PQR. Find the area of the square ABCD.
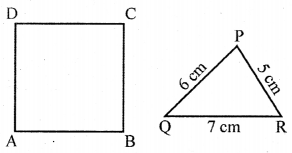
Solution:
Perimeter of ∆PQR = 6 cm + 5 cm + 7 cm = 18 cm
Perimeter of square = 2 × 18 = 36 cm
Side of square = ?
4 × side = 36
⇒ Side = \(\frac{36}{4}\) = 9
Area of square = (side)2 = (9)2 = 9 × 9 = 81 cm2
Question 3.
A wire is in the shape of a square of side 10 cm. If the wire is rebent into a rectangle of length 12 cm, find its breadth. Which encloses more area, the square or the rectangle and by how much?
Solution:
Side of square = 10 cm
Perimeter of square = 4 × 10 cm = 40 cm
According to question,
Perimeter of rectangular = 2(l + b)
⇒ 40 cm = 2 (12 cm + b)
⇒ 40 cm = 24 cm + 2b
⇒ 2b = 40 cm – 24 cm
⇒ 2b = 16 cm
⇒ b = \(\frac{16}{2}\) cm = 8 cm
Area of square = (a)2 = (10 cm)2 = 100 cm2
Area of rectangular = (l × b) = 12 × 8 = 96 cm2
Area of square is more and it is = 100 cm2 – 96 cm2 = 4 cm2
Question 4.
A rectangular room is 9 m long and 6 m wide. Find the cost of covering the floor with carpet 2 m wide at ₹35 per metre.
Solution:
Length of room = 9m
Width of room = 6m
Area of room = l × b = 9 × 6 = 54 m2
Width of carpet = 2m
Area of carpet = 54 m2
Length = ?
Length of carpet = \(\frac{54}{2}\) = 27 m
Cost of covering = ₹35 × 27 m = ₹945
Question 5.
If the cost of fencing a square plot at the rate of ₹ 2.50 per metre is ₹ 200, then find the length of each side of the field.
Solution:
Total cost of fencing a square plot = ₹200
Rate of fencing = ₹2.50
∴ Perimeter of square = \(\frac{\text { Total cost }}{\text { Rate }}\) = \(\frac{200}{2.5}\) = 80m
Since, we know that,
Perimeter of square = 4a
⇒ 80 m = 4a
⇒ a = 20 m
∴ Length of a square plot = 20 m
Question 6.
If the cost of fencing a rectangular park at the rate of ₹7.50 per metre is ₹600 and the length of the park is 24 m, find the breadth of the park.
Solution:
Cost of fencing a rectangular park = ₹600
Rate of fencing = ₹7.50
Perimeter of a park = \(\frac{\text { Total cost }}{\text { Rate }}\) = \(\frac{600}{7.5}\) = 80m
Length of the park = 24 cm
Let breadth of the park = b
∴ Perimeter of a square = 80 m
⇒ 2(l + b) = 80 m
⇒ 2(24 + b) = 80 m
⇒ 24 + b = 80 m
⇒ b = 40 – 24 m
∴ b = 16 m
Question 7.
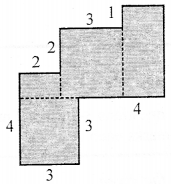
By splitting the following figures into rectangle, find their areas (The measures are given in centimetres).
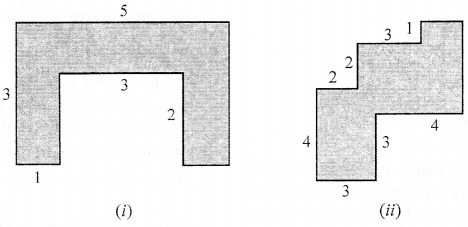
Solution:
(a) Area of the figure,
= (3 × 1 + 3 × 1 + 3 × 1) sq m
= (3 + 3 + 3) sq m
= 9 sq m
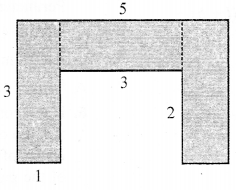
(b) Area of the figure,
= (3 × 3 + 1 × 2 + 3 × 3 + 4 × 2) sq cm
= (9 + 2 + 9 + 8) sq cm
= 28 sq cm