ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Check Your Progress

by

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Check Your Progress

Question 1.
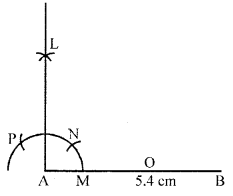
Draw a line segment AB = 5.4 cm. Construct a perpendicular at A by using ruler and compass.
Solution:
Steps of construction:

  1. Draw AB = 5.4 cm.
  2. With any radius draw an arc which cuts AB at M.
  3. With M as centre and the same radius
    cut the previous arc at N and P.
  4. With N and P as centres draw arcs which intersect at L.
    Join AL.
  5. AL is required perpendicular.
    ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Check Your Progress 1

Question 2.
Draw a line segment PQ = 6.8 cm. Draw a perpendicular to it from a point A outside PQ by using ruler and compass.
Solution:
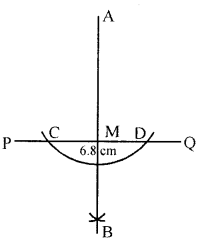
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Check Your Progress 2
Steps of construction:

  1. Draw a line segment PQ = 6.8 cm
    and take a point A outside PQ.
  2. With A as centre and any suitable radius,
    draw an arc to cut line PQ at point C and D.
  3. With C and D as centres,
    draw two arcs of equal radius cutting each other
    at B on the other side of line PQ.
  4. Join AB to meet the line PQ at M.

Question 3.
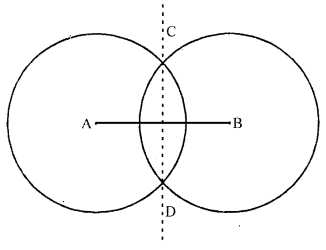
Draw a line segment of length 6.5 cm and construct its axis of symmetry.
Solution:
Steps of construction:

  1. Draw a line segment \(\overline{\mathrm{AB}}\) of length 6.5 cm.
  2. With A as centre, using a compass, draw a circle.
    The radius of this circle should be more than half of the length of \(\overline{\mathrm{AB}}\).
  3. With the same radius and with B as centre,
    draw another circle using a compass.
    Let it cut the previous circle at C and D.
  4. Join CD. Then, \(\overline{\mathrm{CD}}\) is the axis of symmetry of \(\overline{\mathrm{AB}}\).
    ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Check Your Progress 3

Question 4.
Draw ∠AOB = 76° with help of a protractor. Bisect this angle by using ruler and compass. Measure the two parts by your protractor and see how accurate you are.
Solution:
Steps of construction:

  1. Draw a line segment OB.
  2. Construct ∠AOB with the help of protector = 76°.
  3. With the help of compass and O as centre
    draw an arc meeting OB and OA at P and Q respectively.
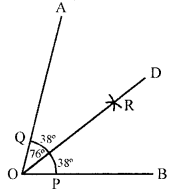
    ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Check Your Progress 4
  4. With P and Q as centre and radius more than \(\frac{1}{2}\) PQ
    draw two arcs meeting each other at R.
  5. OD is the bisector of ∠AOB.
  6. On measuring ∠AOD = ∠DOB = 38°.

Question 5.
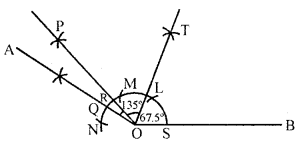
By using and compass, construct an angle of 135° and bisect it. Measure any one part by protractor and see how accurate you are.
Solution:
Steps of construction:

  1. Draw a line OB with help of ruler.
  2. With O as a centre and any suitable radius
    draw an arc to meet OB at S.
  3. With S as a centre and same radius
    draw an arc to meet the previous arc at L.
    With L as centre and same radius draw another arc M.
    Again M as centre draws another arc to meet the first arc at N.
  4. With M and N as centres draw two arcs of
    equal radius \(\left(>\frac{1}{2} \mathrm{SL}\right)\) cutting each other at A.
  5. Join OA intersecting the radius at point Q.
  6. Now taking Q and M as a centres
    draw two arcs of equal radius cutting each other at P.
  7. Join PO.
  8. Measuring the ∠POB with protractor we get ∠POB equal to 135°.
  9. Taking S and R as a centres draw two arcs cutting each other at T.
    Join TO.
  10. ∠TOB is the bisector of ∠POB. ∠TOB = ∠TOP = 67.5°.
    ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 13 Practical Geometry Check Your Progress 5

ML Aggarwal Class 6 Solutions for ICSE Maths

Leave a Comment