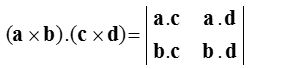Dot Product

Dot Product

Scalar or Dot product

(1) Scalar or Dot product of two vectors:
If a and b are two non-zero vectors and θ be the angle between them, then their scalar product (or dot product) is denoted by a.b and is defined as the scalar |a||b| cos θ , where |a| and |b| are modulii of a and b respectively and 0≤ θ≤π. Dot product of two vectors is a scalar quantity.

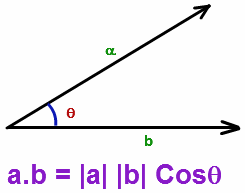
Angle between two vectors:
If a, b be two vectors inclined at an angle θ, then a.b = |a||b| cos θ.

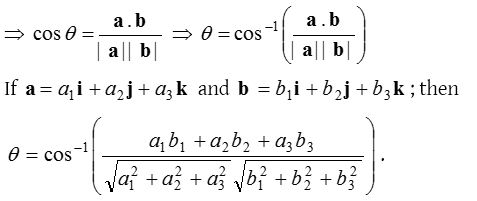
(2) Properties of scalar product:

1. Commutativity: The scalar product of two vector is commutative i.e., a . b = b . a.
2. Distributivity of scalar product over vector addition: The scalar product of vectors is distributive over vector addition i.e.,
   (a) a.(b + c) = a . b − a . c, (Left distrihutivity)
   (b) (b + c).a = b . a + c . a , (Right distrihutivity)
3. Let a and b be two non-zero vectors a . b = 0 ⇔ a ⊥ b.
   As i, j, k are mutually perpendicular unit vectors along the co-ordinate axes, therefore, i . j = j . i =0 ; j . k = k . j = 0; k . i = i . k = 0.
4. For any vector a, a . a = |a|².
   As i, j, k are unit vectors along the co-ordinate axes, therefore i . i = |i|², j . j = |j|² and k . k = |k|²
5. If m, n are scalars and a, b be two vectors, then ma . nb = mn(a . b) = (mn a).b = a.(mn b)
6. For any vectors a and b, we have
   (a) a. (−b) = − (a.b) = (−a).b
   (b) (−a).( −b) = a.b
7. For any two vectors a and b, we have
   1. |a + b|² = |a|² + |b|² + 2a.b
   2. |a − b|² = |a|² + |b|² + 2a.b
   3. (a+b).(a—b) = |a|² − |b|²
   4. |a + b| =  |a| + |b| ⇒ a ∥ b
   5. |a + b|² = |a|² + |b|² ⇒ a ⊥ b
   6. |a + b| = |a − b| = ⇒ a ⊥ b

(3) Scalar product in terms of components:
If a = a₁i + a₂j + a₃k and b = b₁i + b₂j + b₃k then a . b = a₁b₁ + a₂b₂ + a₃b₃.

The components of b along and perpendicular to are and respectively.

(4) Work done by a force:

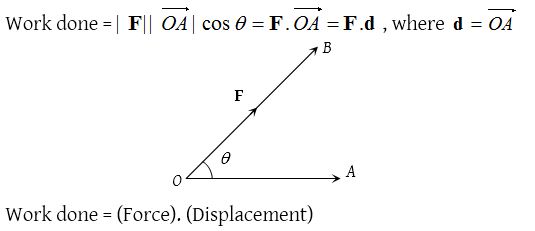
If a number of forces are acting on a particle, then the sum of the works done by the separate forces is equal to the work done by the resultant force.

Scalar triple product

(1) Scalar triple product of three vectors:
If a, b, c are three vectors, then their scalar triple product is defined as the dot product of two vectors a and b × c. It is generally denoted by a . (b × c) or [a b c].

(2) Properties of scalar triple product:

1. If a, b, c are cyclically permuted, the value of scalar triple product remains the same. i.e., (a × b). c = (b × c). a = (c × a). b or [a b c] = [b c a] = [c a b]
2. The change of cyclic order of vectors in scalar triple product changes the sign of the scalat’ triple product but not the magnitude i.e., [a b c] = −[b a c] = −[c b a] = −[a c b]
3. In scalar triple product the positions of dot and cross can be interchanged provided that the cyclic order of the vectors remains same i.e., (a × b). c = a. (b × c)
4. The scalar triple product of three vectors is zero if any two of them are equal.
5. For any three vectors a, b, c and scalar λ, [λ a b c] = λ[a b c]
6. The scalar triple product of three vectors is zero if any two of them are parallel or collinear.
7. If a, b, c, d are four vectors, then [(a + b) c d] = [a c d] + [b c d].
8. The necessary and sufficient condition for three non-zero non-collinear vectors to be coplanar is that [a b c] = 0.
9. Four points with position vectors a, b, c and d will be coplanar, if [ a b c] + [d c a] + [d a b] = [a b c].
10. Volume of parallelopiped whose coterminous edges are a, b, c is [a b c] or a(b × c).

(3) Scalar triple product in terms of components:

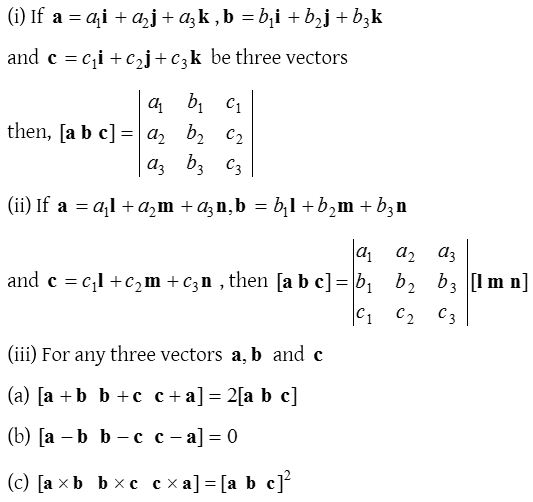
(4) Tetrahedron:
A tetrahedron is a three-dimensional figure formed by four triangle OABC is a tetrahedron with ∆ABC as the base. OA, OB, OC, AB, BC and CA are known as edges of the tetrahedron. OA, BC; OB, CA and OC, AB are known as the pairs of opposite edges. A tetrahedron in which all edges are equal, is called a regular tetrahedron. Any two edges of regular tetrahedron are perpendicular to each other.

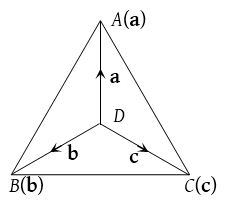
Volume of tetrahedron

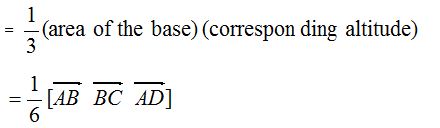
1. The volume of a tetrahedron
2. If a, b, c are position vectors of vertices A, B and C with respect to O, then volume of tetrahedron OABC = \(\frac { 1 }{ 6 }\) [a b c].
3. If a, b, c, d are position vectors of vertices A, B, C, D of a tetrahedron ABCD, then its volume = \(\frac { 1 }{ 6 }\) [b−a c−a d−a].

(5) Reciprocal system of vectors:
Let be three non-coplanar vectors, and let 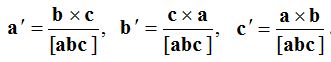. a‘, b‘, c‘ are said to form a reciprocal system of vectors for the vectors a, b, c.
If a, b, c and a‘, b‘, c‘ form a reciprocal system of vectors, then

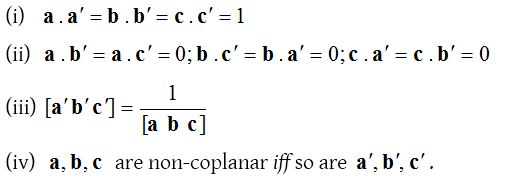
Scalar product of four vectors

(a × b) . (c × d) is a scalar product of four vectors. It is the dot product of the vectors a × b and c × d.
It is a scalar triple product of the vectors a,b and c × d as well as scalar triple product of the vectors a × b, c and d.