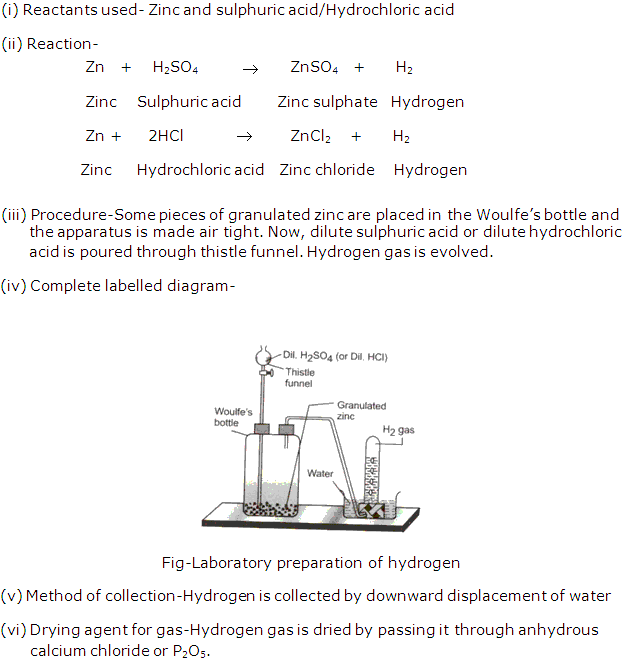
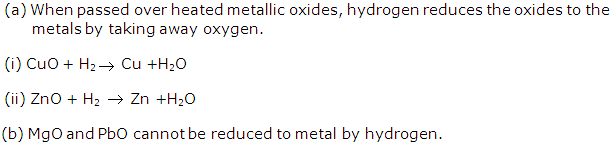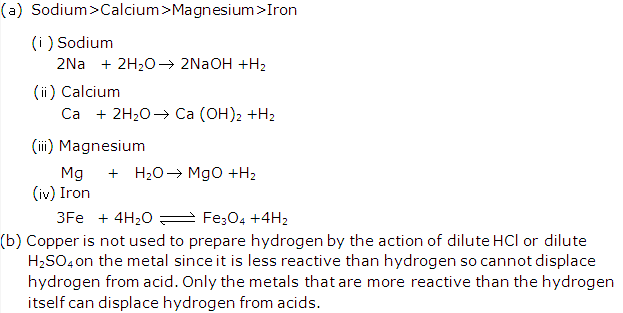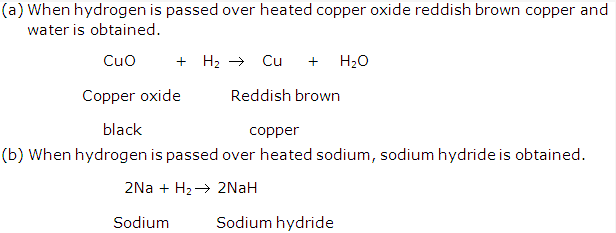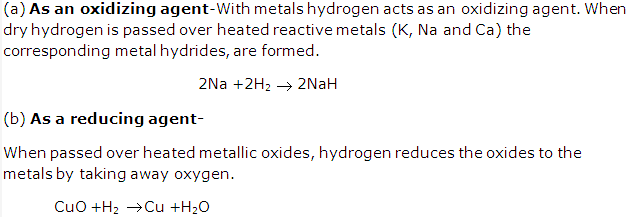Frank ICSE Solutions for Class 9 Chemistry – Water
PAGE NO :96
Solution 1:
The molecular formula of water is H2O, this shows that water is not an element but it is a compound made up of two elements hydrogen and oxygen combined in a fixed ratio, i.e., 1:8 by mass. This also shows that the properties of water is totally different from those of hydrogen and oxygen as compounds have completely different properties than the elements of which it is made up of.
Solution 2:
Two characteristics properties responsible for making water a good solvent are:
- Water molecule can form hydrogen bonds with the molecules of other compounds.
- Water molecule is polar in nature.
Solution 3:
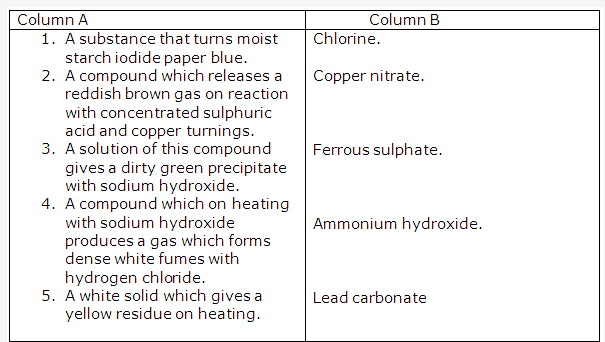
Solution 4:
- (a) Physical properties of water:
- Pure water is colourless, transparent, odourless and tasteless liquid.
- Boiling and Freezing points: At normal atmospheric pressure water boils at 100oC and freezes at 0oC.
- Pure water being a covalent compound is a very poor conductor of heat and electricity.On addition of electrolytes it becomes a good conductor of heat and electricity.
- Solvent properties:Water is a remarkable solvent dissolves many substances forming aqueous solutions because of its high dielectric constant.
- Anomalous behavior: On cooling water contracts in volume, as do other liquids, but at 4o C, it starts expanding, and continues to do till the temperature reaches 0oC,the point at which it converts to ice.
- (b)
- Boiling point of water: It increases with the addition of salt in water.
- Freezing point of water: It decreases with the addition of salt in water.
- Density of water: It increases with the addition of salt in water.
Solution 5:
Due to its high specific heat capacity, water is used in cooling systems for e.g., as coolant in motor car radiators.
Solution 6:

Solution 7:
- (a) Water reacts with metals oxides: corresponding hydroxides are formed which act as alkalis.
- (b) Water reacts with non metals oxides: corresponding acids are formed.
Solution 8:
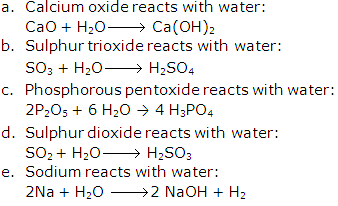
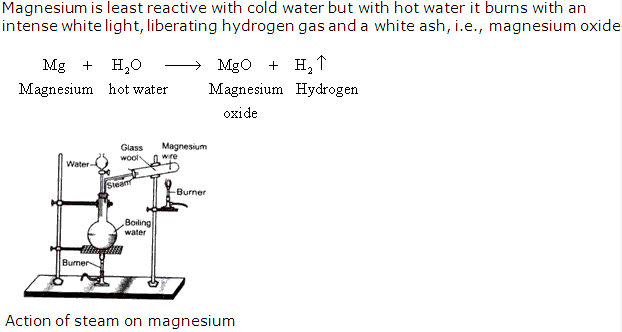
Solution 9:
We can test the odourless, colourless liquid by:
- Measuring its boiling point, if comes out to be 100 oC then it confirms the liquid to be water.
- Measuring its melting point, if comes out to be 0 oC then it confirms the liquid to be water.
Solution 10:

Solution 11:
- (a) Water being the universal solvent ,acts as an important mode of transport in plants,also water taken from natural source contains dissolved salts in them which is essential for the growth and development of plants
- (b) Water constitutes 3/4th of our human body and it is necessary for the survival of human beings and being the universal solvent helps in transportation and also regulates the body temperature.It also contains dissolved salts which supply essential minerals which are necessary for our body.
Solution 12:

Solution 13:
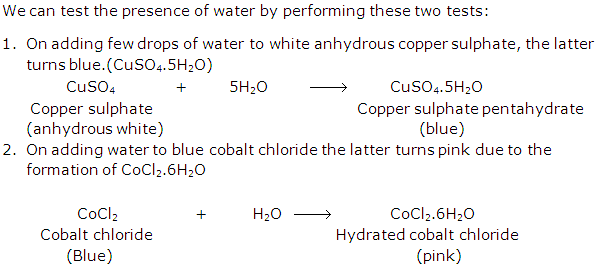
Solution 14:
Density of water is 0.997 gcm-3 at 4oC . The density of water decreases when the temperature increases above 4oC or decreases below 4oC.
At 40C, water has its maximum density and minimum volume. At any temperatur above or below 4 C, the density of water decreases. This property is called anomalous expansion of water. The significance of this unique property of water is that it enables marine life to exist in the colder regions of the world, because even when water freezes on the top, it is still liquid below the ice layer.
Solution 15:
At 40C, water has its maximum density and minimum volume. The property of anomalous expansion of water enables marine life to exist in the colder regions of the world because even when water freezes on the top, it is still liquid below the ice layer.
PAGE NO :97
Solution 16:
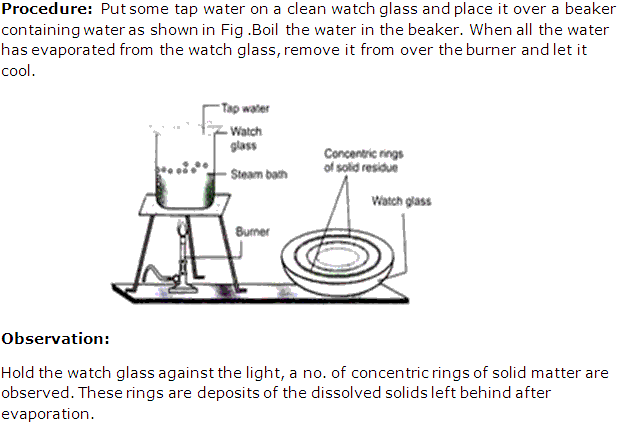
Solution 17:

Solution 18:
- (a) Liquids: alcohols, acids
- (b) Solids: Sugar, urea
- (c) Gases: Oxygen, carbon dioxide
Solution 19:
Rain water is the purest form of natural water.
Solution 20:
- (a) Solid in a liquid: Solubility decreases with rise in temperature in an exothermic process, for example, calcium sulphate(CaSO4), sodium sulphate(NaSO4), and in an endothermic reaction solubility increases with rise in temperature,for example potassium nitrte(KNO3) and sodium nitrate(NaNO3).
- (b) A gas in a liquid: Solubility decreases with rise in temperature.Thus, gases dissolves readily in cold water than in hot water.
Solution 21:
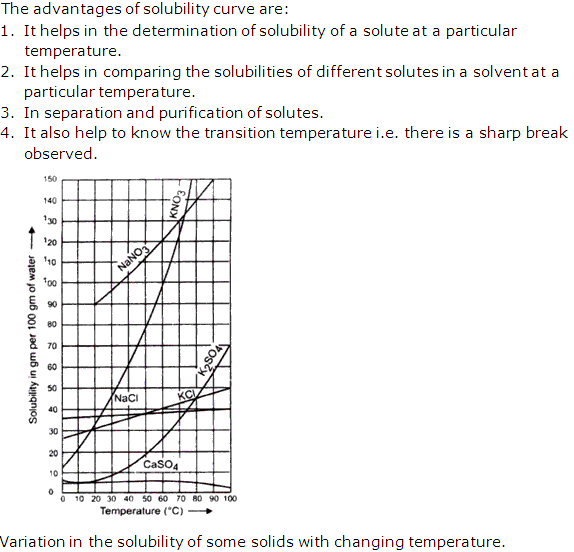
Solution 22:
- (a) Density of water is 0.997 gcm-3 at 4oC .The density of water decreases when the temperature decreases below 4oC. So ice has less density of 0.92 and is lighter then that of water hence it floats on water.
- (b) A solution is said to be saturated if at a particular temperature if no more of the solute can be dissolved in it at that temperature, when the temperature is increased more solute particles can be dissolved in that saturated solution as the solubility of most of the substances generally increases with rise in temperature and thereby making it unsaturated.
- (c) Solubility of gases decreases with increase in temperature hence hot water contains less dissolved air than cold water.
Solution 23:
- (a) Solute: The substance which dissolves in a medium to produce a solution is called the solute.
- (b) Solvent: It is the medium in which the solute dissolves.
- (c) Solution: A homogeneous mixture that has a uniform composition throughout the volume of the mixture. It is the medium in which the solute dissolves.
Solution 24:
- (a) When we heat a saturated solution more solute can be dissolved in it, it as mostly solubility increases on raising the temperature and the solution then becomes an unsaturated solution.
- (b) When a hot saturated solution is cooled slowly and is kept undisturbed the excess salt does not separates out . Thus the solution becomes a supersaturated solution which contains more solute in it than it can hold at room temperature.
- (c) When the quantity of solvent increases,greater amount of solute can be dissolved.
Solution 25:
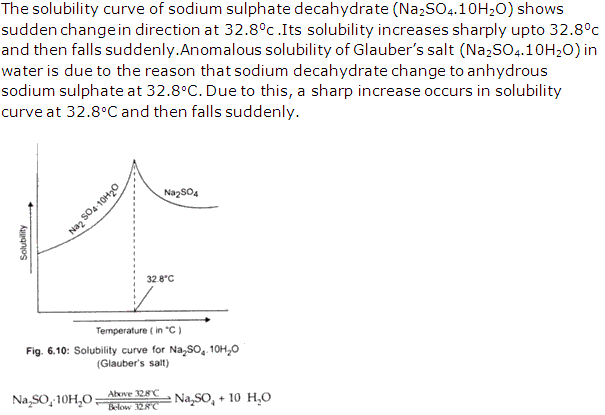
Solution 26:
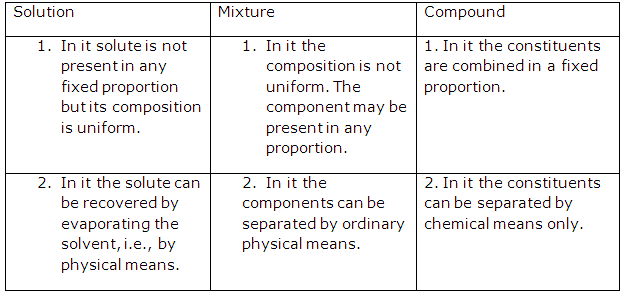
Solution 27:
Solubility of a solid depends on:
- Size of particles: Smaller the size of particles of the solute, greater is the solubility.
- Contact between solute and the solvent: Increased contact between the solute and the solvent increases the solubility.
- Temperature: The variation of solubility with temperature depends on its nature i.e. whether the reaction is exothermic or endothermic.
For exothermic reactions-The solubility decreases on increasing the temperature.
For endothermic reaction-The solubility increases on increasing the temperature.
Solution 28:
Henry’s law states that:
At a constant temperature, the amount of a given gas that dissolves in a given type and volume of liquid is directly proportional to the partial pressure of that gas in equilibrium with that liquid.
Solution 29:
- Z is least reactive so it will be found free in nature.
- X is more reactive so it will react with oxygen more readily and with ease.
- Z
- Y is iron whose oxide is brown coloured Fe2O3.
- X
- The piece of Y i.e., iron is more reactive then copper so it will displace copper from copper nitrate and a brown layer of copper will be developed on the iron piece.
Solution 30:
Drop in, a crystal of the solute that is in the solution. If the crystal dissolves its unsaturated, if it stays the same size then its saturated and if it gets bigger than its supersaturated.
- This is because an unsaturated solution will be able to take in more solute, so it dissolves the crystal.
- A saturated solution will not take in more solute but will also not deposit any solute so the crystal stays the same size.
- A supersaturated solution wants to deposit its excess solute and become saturated, it just needs something to start it along.
The crystal starts it up and it will deposit its excess solute onto the crystal making the crystal bigger.
PAGE NO :98
Solution 31:
- (a) Increase in weight: when sodium chloride when exposed in air it gains moisture and its weight increases.
- (b) Decrease in weight: iron when exposed to air gets rusted due to the presence of moisture in the air it gets corroded, and hence its weight is reduced.
- (c) No effect on weight: when conc. Sulphuric acid when exposed to air does not react and no change occurs in weight.
Solution 32:
Water pollution may be defined as the contamination of water by foreign substances which make it harmful for health of animals or plants or aquatic life, make it unfit for drinking and for domestic, industrial and agriculture use.
Solution 33:
Major pollutants of water are:
Ground water pollutants: Septic tanks, industry by products like pesticides, fertilizers, tanneries, mining wastes.
Surface water pollutants: No. of gases present in atmosphere like SO2, CO2, H2S, NOx, CO, etc., pollute surface water.
Lake water pollutant: organic wastes from hills, toxic effluents from urban areas, industrial effluents, dumping of huge amounts of sediments etc.,
River water pollutants: Industrial discharge, sewage discharges, detergents, discharges from drug, paper, and textile industries
Marine water pollutant: major pollutant is oil spills.
Solution 34:
Various sources of water pollution are:
- Natural process: Washing away of decomposed and animal wastes into main stream of water.
- Human activity:
- (a)Discharge of Household detergents: detergents used as a cleaning agent produce foam and pollute water. They do not undergo bio-degradation.
- (b) Discharge of industrial effluents: Industrial activities generate a variety of waste products which are generally discharged into water streams.The pollutants associated with the industrial effluents are organic matter, inorganic dissolved salts, suspended solids. They inhibit oxidation or organic compounds; stabilize the colloidal impurities which do not aggregate to settle down.
- (c) Sewage: Sewage is cloudy dilute aqueous solution containing minerals and organic matter.Sewage from homes and industries contains decomposable organic matter ,inorganic cations and anions,toxic metals etc.Pouring the drains and sewers in fresh water bodies causes water pollution.
Water pollution due to sewage creates the following problems:- Self purifying ability of water is lost and it becomes unfit for domestic purpose.
- Self regulatory capabilities of aquatic organism is retarded.
- Sewages produce pathogens which are diseases causing bacteria and result in water born gastro-intestinal diseases.
Solution 35:
Water treated for safe effluents involves sequential treatment:
- Primary treatment: The primary treatment involves physico-chemical processes to reduce settle able suspended solids of the wastes water and smoothened out individual effluent flow variations.It involves physic-chemical processes such as sedimentation,aeration,adsorption,oxidation etc.
- Secondary treatment: In this, the dissolved and colloidal organic matter present in waste is removed by biological processes involving bacteria and other micro organisms.
These process may be aerobic or anaerobic.
Aerobic treatment: Purification is carried out by aerobes in the presence of molecular oxygen.
Anaerobic treatment: Purification of waste is achieved by anaerobes in complete absence of molecular oxygen. - Tertiary treatment: It is the final treatment for polishing the effluents from secondary treatment. By this process suspended solids are removed, bacteria are removed, and organic and inorganic solids are removed.
Solution 36:
Two water born diseases are:
- Gastroenteritis
- Bacterial dysentery