Areas Of Parallelograms And Triangles

- Parallelograms on the same base and between the same parallels are equal in area.
- Area of a parallelogram is the product of its any side and the corresponding altitude.
- Parallelogram on the same base and having equal areas lie between the same parallels.
- If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle, is half the area of the parallelogram
- Two congruent figures having same area.
- Triangles on the same base and between the same parallels are equal in area.
- The area of a triangle is half the product of any of its sides and the corresponding altitude.
- If a triangle and a parallelogram are on the same base and between the same parallels, the area of the triangle is equal to half of the parallelogram.
- The area of a trapezium is half the product of its height and the sum of parallel sides.
- Triangles having equal areas and having one side of one of the triangles equal to one side of the other, have their corresponding altitudes equal.
Areas Of Parallelograms And Triangles Example Problems With Solutions
Example 1: ABCD is a quadrilateral and BD is one of its diagonals as shown in fig. Show that ABCD is a parallelogram and find its area.
Solution: Since diagonal BD intersects transversals AB and DC at B and D respectively such that
∠ABD = ∠CDB [Each equal to 90°]
i.e., alternate interior angles are equal.
∴ AB || DC
Also, AB = DC [Each equal to 5.2 cms (Given)]
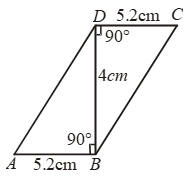
Thus, one pair of opposite sides AB and DC of quadrilateral ABCD are equal and parallel.
Hence, ABCD is a parallelogram.
Now
ar (||gm ABCD) = Base × Corresponding altitude
= AB × BD = 5.2 × 4 sq.cm
Example 2: In parallelogram ABCD, AB = 10 cm. The altitudes corresponding to the sides AB and AD are respectively 7 cm and 8 cm. Find AD.
Solution: We have,
Area of a ||gm = Base × Height.
∴ ar (||gm ABCD) = AB × DM
= (10 × 7) cm2 …. (i)
Also, ar (||gm ABCD) = AD × BN
= (AD × 8) cm2 ….(ii)
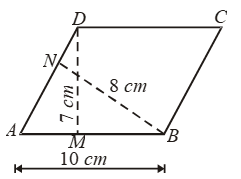
From (i) and (ii), we get
10 × 7 = AD × 8
⇒ AD = 70/8 = 8.75 cm.
Example 3: In the adjoining figure, ABCD is a ||gm whose diagonals AC and BD intersect at O. A line segment through O meets AB at P and DC at Q. Prove that are (ΔAPQD) = 1/2 ar (||gm ABCD).
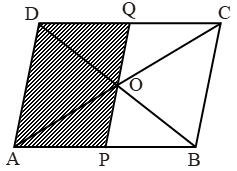
Solution: Diagonal AC of ||gm ABCD divides it into two triangles of equal area.
∴ ar(∆ACD) = 1/2 ar(||gm ABCD) ….(i)
In ∆OAP and OCQ, we have
OA = OC
[diagonals of a ||gm bisect each other]
∠AOP = ∠COQ [vert. opp. ∠]
∠PAO = ∠QCO [alt. int. ∠]
∴ ∆OAP ≅ ∆OCQ
∴ ar(∆OAP) = ar(∆OCQ)
⇒ ar(∆OAP) + ar(quad. AOQD)
= ar(∆OCQ) + ar(quad. AOQD)
⇒ ar(quad. APQD) = ar(∆ACD)
= 1/2 ar(||gm ABCD) [using (i)]
∴ ar(∆APQD) = 1/2 ar(||gm ABCD)
Example 4: Show that a median of a triangle divides it into two triangles of equal area.
Solution: Given: A ∆ ABC in which AD is the median.
To Prove: ar (∆ABD) = ar (∆ADC)
Construction: Draw AL ⊥ BC.
Proof Since AD is the median of ∆ ABC. Therefore,
D is the mid-point of BC.
⇒ BD = DC
⇒ BD × AL = DC × AL
[Multiplying both sides by AL]
⇒ 1/2 (BD × AL) = 1/2 (DC × AL)
⇒ ar (∆ABD) = ar (∆ADC)
ALITER: Since ∆s ABD and ADC have equal bases and the same altitude AL. Therefore,
ar (∆ ABC) = ar (∆ ADC).
Example 5: In figure, AD is a median of ∆ABC and DE is a median of ∆DAC. Show that
ar(∆AED) = 1/4 ar(∆ABC)
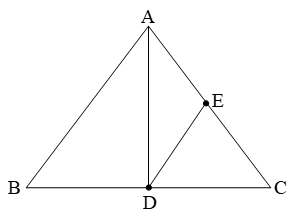
Solution:
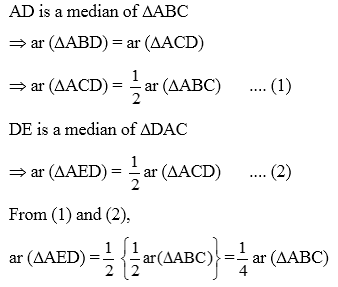
Example 6: The diagonals of ABCD, AC and BD intersect in O. Prove that if BO = OD, the triangles ABC and ADC are equal in area.
Solution: Given: A quadrilateral ABCD in which its diagonals AC and BD intersect at O such that BO = OD.
To Prove: ar (∆ ABC) = ar (∆ ADC)
Proof: In ∆ ABD, we have BO = OD. [Given]
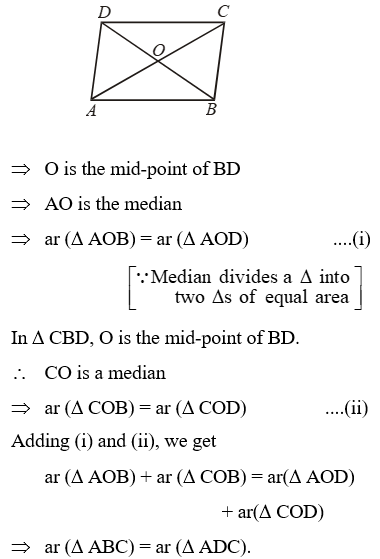
Example 7: Let P, Q, R, S be respectively the midpoints of the sides AB, BC, CD and DA of quad. ABCD. Show that PQRS is a parallelogram such that ar(||gm PQRS) = ar(quad. ABCD).
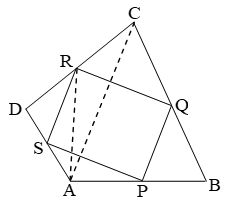
Solution:



Example 8: The medians BE and CF of a triangle ABC intersect at G. Prove that area of ∆GBC = area of quadrilateral AFGE.
Solution: Join EF. Since the line segment Joining the mid-points of two sides of a triangle is parallel to the third side. So, EF || BC.
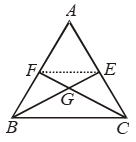
Clearly, ∆sBEF and CEF are on the same base EF and between the same parallel lines. So,
ar (∆BEF) = ar (∆CEF)
⇒ ar (∆BEF) – ar (∆GEF) = ar (∆CEF) – ar (∆GEF)
⇒ ar (∆BFG) = ar (∆CEG) …. (i)
We know that a median of a triangle divides it into two triangels of equal area.
Therefore,
ar (∆BEC) = ar (∆ABE)
⇒ ar(∆BGC) + ar (∆CEG) = ar(quad. AFGE) + ar (∆BFG)
⇒ ar(∆BGC) + ar(∆BFG) = ar (quad. AFGE) + ar (∆BFG) [Using (i)]
⇒ ar (∆BGC) = ar (quad. AFGE)
Example 9: E, F, G, H are respectively, the mid-points of the sides AB, BC, CD and DA of parallelogram ABCD. Show that the area of quadrilateral EFGH is half the area of the parallelogram ABCD.
Solution: Given: A quadrilateral ABCD in which E, F, G, H are respectively the mid-points of the sides AB, BC, CD and DA.
To Prove:
(i) ar (||gm EFGH) = 1/2 ar (||gm ABCD)
Construction: Join AC and HF
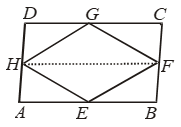
Since ∆HGF and ||gm HDCF are on the same base HF and between the same parallel lines.
∴ ar(∆HGF) = 1/2 ar (||gm HDCF) ….(i)
Similarly, ∆HEF and ||gm HABF are on the same base HF and between the same parallels.
∴ar (∆HEF) = 1/2 ar (||gm HABF) ….(ii)
Adding (iii) and (iv),we get
ar (∆HGF) + ar (∆HEF)
= 1/2 [ar(||gm HDCF) + ar( ||gm HABF)]
⇒ ar (||gm EFGH) = 1/2 ar (||gm ABCD).
Example 10: Two segments AC and BD bisect each other at O. Prove that ABCD is a parallelogram.
Solution: Given: AC and BD are two segments bisecting each other at O.
To Prove: ABCD is a parallelogram.
Construction: Join AB, BC, CD and DA.
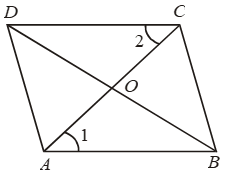
Proof: In ∆s AOB and COD, we have
AO = CO [Given]
BO = DO [Given]
and, ∠AOB = ∠COD [Vertically opp. ∠s]
So, by SAS criterion of congruence
∆AOB ≅ ∆COD
⇒ AB = CD [∵ Corresponding parts of congruent triangles are equal]
and, ∠1 = ∠2.
Thus, AB and DC intersect AC at A and C respectively such that
∠1 = ∠2 i.e. alternate interior angles are equal.
∴ AB || DC
Thus, in quadrilateral ABCD, we have
AB = DC and AB || DC
i.e. a pair of opposite sides are equal and parallel.
Hence, ABCD is a parallelogram.
Example 11: ABCD is a parallelogram. L and M are points on AB and DC respectively and AL = CM. Prove that LM and BD bisect each other.
Solution: We have, AL = CM
⇒ AB – BL = CD – DM
⇒ – BL = – DM [∵ ABCD is a parallelogram ∴ AB = DC]
⇒ BL = DM …. (i)
Now, AB || DC and transversals BD and LM intersect them.
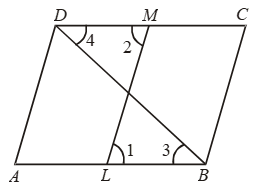
∴ ∠3 = ∠4 and ∠1 = ∠2 ….(ii)
Thus, in ∆s OBL and ODM, we have
∠1 = ∠2 [From (ii)]
BL = MD [From (i)]
∠3 = ∠4 [From (ii)]
So, by ASA criterion of congruence
∆OBL ≅ ∆ODM
⇒ OB = OD and OL = OM
[∵ Corresponding parts of congruent triangles are equal]
⇒ O is the mid-point of BD and LM both.
⇒ BD and LM bisect each other.
Example 12: A point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles.
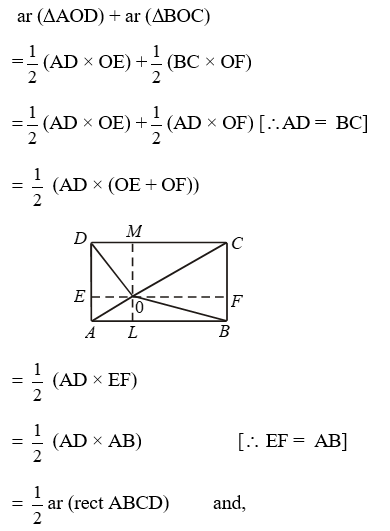
Solution: Given: A rectangle ABCD and O is a point inside it, OA, OB, OC and OD have been joined.
To Prove: ar (∆AOD) + ar (∆BOC)
= ar (∆AOB) + ar (∆COD).
Construction: Draw EOF|| AB and LOM || AD.
Proof: We have,

Example 13: ABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD, DA respectively. Prove that PQRS is a rectangle.
Solution: Given: A rhombus ABCD in which P, Q, R, S are the mid-points of sides AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined.
To Prove: PQRS is rectangle.
Construction: Join AC.
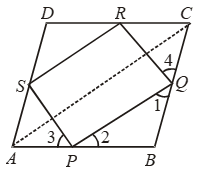
Proof: In order to prove that PQRS is a rectangle, it is sufficient to show that it is a parallelogram whose one angle is a right angle. First we shall prove that PQRS is parallelogram.
In ∆ABC, P and Q are the mid-points of AB and BC respectively.
∴ PQ || AC and PQ = 1/2 AC ….(i)
In ∆ADC, R and S are the mid-points of CD and AD respectively.
∴ RS || AC and RS = 1/2 AC ….(ii)
From (i) and (ii), we have
PQ || RS and PQ = RS
Thus, PQRS is a quadrilateral such that one pair of opposite sides PQ and SR is equal and parallel.
So, PQRS is a parallelogram.
Now, we shall prove that one angle of parallelogram PQRS is a right angle.
ABCD is a rhombus
⇒ AB = BC
[∵ All sides of a rhombus are equal]


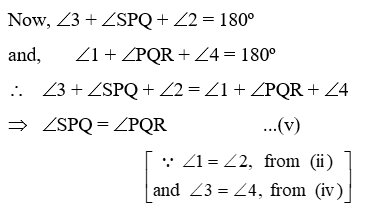
Now, transversal PQ cuts parallel lines SP and RQ at P and Q respectively.
∴ ∠SPQ + ∠PQR = 180º
⇒ ∠SPQ + ∠SPQ = 180º [Using (v)]
⇒ ∠SPQ = 90º
Thus, PQRS is a parallelogram such that ∠SPQ = 90º.
Hence, PQRS is a rectangle.
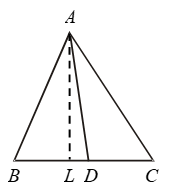
Example 14: Triangles ABC and DBC are on the same base BC with A, D on opposite sides of line BC, such that ar (∆ ABC) = ar (∆ DBC). Show that BC bisects AD.
Solution: Since ∆s ABC and DBC are equal in area and have a common side BC. Therefore the altitudes corresponding to BC are equal i.e.
AE = DF.
Now, in ∆s AEO and DFO, we have
∠1 = ∠2 [Vertically opp. angles]
∠AEO = ∠DFO [Each equal to 90°]
and, AE = DF
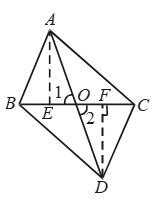
So, by AAS criterion of congruence,
∆ AEO ≅ ∆ DFO
⇒ AO = DO
⇒ BC bisects AD.
Example 15: ABCD is a parallelogram and O is any point in its interior. Prove that:
(i) ar (∆AOB) + ar (∆COD) = 1/2 ar (parallelogram ABCD)
(ii) ar (∆AOB) + ar ∆(COD) = ar (∆BOC) + ar (∆AOD)
Solution: Given: A parallelogram ABCD and O is a point in its interior.
(i) Since ∆AOB and parallelogram ABFE are on the same base AB and between the same parallel lines AB and EF.
∴ ar (∆AOB) = 1/2 ar (parallelogram ABFE) ….(i)
Similarly,
ar (∆COD) = 1/2 ar (parallelogram DEFC) ….(ii)
Adding (i) and (ii), we get
ar (∆AOB) + ar (∆COD) = 1/2 ar (parallelogram ABCD)
(ii) To Prove: ar(∆AOB) + ar(∆COD)
= ar (∆BOC) + ar (∆AOD).
Construction: Draw EOF ||AB and GOH || AD.
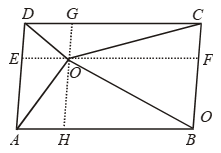
Proof: Since GH || DE and EF || DC
∴ OG || DE and OE || GD
⇒ EOGD is a parallelogram
Similarly, EAHO, HBFO and FOGC are parallelograms.
Now, OD is a diagonal of parallelogram EOGD
⇒ ar (∆EOD) = ar (∆DOG) …. (iii)
OA is a diagonal of parallelogram EAHO
⇒ ar (∆EOA) = ar (∆AOH) ….(iv)
OB is a diagonal of parallelogram HBFO
⇒ ar (∆BOF) = ar (∆BOH) ….(v)
OC is a diagonal of parallelogram FOGC
⇒ ar (∆FOC) = ar (∆COG)
Adding (iii), (iv) and (v), we get
ar (∆EOD) + ar (∆EOA) + ar (∆BOF) + ar(∆FOC)
= ar (∆DOG) + ar (∆AOH) + ar (∆BOH) + ar (∆COG)
⇒ ar (∆AOD) + ar (∆BOC) = ar (∆AOB) + ar (∆COD)
Example 16: A quadrilateral ABCD is such that diagonal BD divides its area in two equal parts. Prove that BD bisects AC.
Solution: Given: A quadrilateral ABCD in which diagonal BD bisects it, i.e.
ar (∆ABD) = ar (∆BDC)
Construction: Join AC.
Suppose AC and BD intersect at O. Draw
AL ⊥ BD and CM ⊥ BD.
To Prove: AO = OC.
Proof: We have, ar (∆ ABD) = ar(∆ BDC)
Thus, ∆s ABD and ABC are on the same base AB and have equal area. Therefore, their corresponding altitudes are equal.
i.e., AL = CM
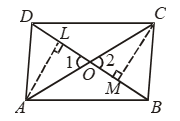
Now, in ∆s ALO and CMO, we have
∠1 = ∠2 [Vertically opposite angles]
∠ALO = ∠CMO [Each equal to 90°]
and, AL = CM [Proved above]
So, by AAS criterion of congruence
∆ALO ≅ ∆CMO
⇒ AO = OC ⇒ BD bisects AC.
Example 17: In Fig. ABCD is a trapezium in which side AB is parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC.
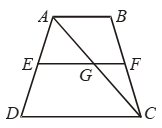
Prove that EF = 1/2 (AB + DC).
Solution: Given: A trapezium ABCD in which AB || DC, E is the mid-point of AD and F is a point on BC such that EF || DC.
To Prove: EF = 1/2 (AB + DC)
Proof: In ∆ADC, E is the mid-point of AD and EG || DC (Given)
∴ G is the mid-point of AC
Since segment joining the mid-points of two sides of a triangle is half of the third side.

Example 18: In ∆ABC, D is the mid-point of AB. P is any point of BC. CQ || PD meets AB in Q. Show that ar (∆BPQ) = 1/2 ar (∆ABC).
Solution: To Prove: ar (∆BPQ) = 1/2 ar (∆ABC)
Construction: Join CD.
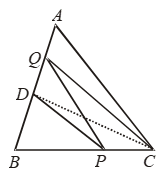
Proof: Since D is the mid-point of AB. So, in ∆ABC, CD is the median.
ar (∆BCD) = 1/2 ar (∆ABC) …. (i)
Since ∆sPDQ and PDC are on the same base PD and between the same parallel lines PD and QC.
∴ ar(∆PDQ) = ar (∆PDC) ….(ii)
Now, from (i)
ar (∆BCD) = 1/2 ar(∆ABC)
⇒ ar (∆BPD) + ar (∆PDC) = 1/2 ar (∆ABC)
⇒ ar (∆BPD) + ar (∆PDQ) = 1/2 ar (∆ABC) [Using (ii)]
⇒ ar (∆BPQ) = 1/2 ar (∆ABC)
Example 19: If the medians of a ∆ABC intersect at
G, show that ar(∆AGB) = ar(∆ AGC) = ar(∆ BGC) = 1/3 ar(∆ ABC).
Solution: Given: A ∆ABC such that its medians AD, BE and CF intersect at G.
To Prove: ar (∆ AGB) = ar (∆ BGC) = ar (CGA) = 1/3 ar (∆ ABC)
Proof: We know that the median of a triangle divides it into two triangles of equal area.
In ∆ ABC, AD is the median
⇒ ar (∆ ABD) = ar (∆ ACD) …. (i)
In ∆ GBC, GD is the median
⇒ ar (∆ GBD) = ar (∆ GCD) ….(ii)
Subtracting (ii) from (i), we get
ar (∆ ABD) – ar (∆ GBD) = ar (∆ ACD) – ar (∆ GCD)
⇒ ar (∆ AGB) = ar (∆ AGC) ….(iii)
Similarly,
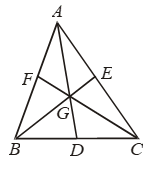
ar (∆ AGB) = ar (∆ BGC) ….(iv)
From (iii) and (iv), we get
ar(∆ AGB) = ar(∆ BGC) = ar(∆ AGC) ….(v)
But, ar (∆ AGB) + ar (∆ BGC) + ar (∆ AGC)
= ar (∆ ABC)
∴ 3 ar (∆ AGB) = 1/3 ar (∆ ABC)
⇒ ar (∆ AGB) = ar (∆ ABC)
Hence, ar (∆ AGB) = ar (∆ AGC) = ar (∆ BGC)
= 1/3 ar (∆ ABC).
Example 20: In a parallelogram ABCD, E, F are any two point on the sides AB and BC respectively. Show that ar (∆ADF) = ar (∆DCE).
Solution: Construction: Draw EG || AD and FH || AB.
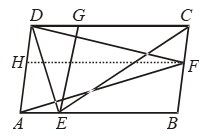
Proof: Since FH || AB (by construction). Therefore, ABFH is a parallelogram.


Example 21: In Fig. PQRS is a parallelogram, PQ and QO are respectively, the angle bisectors of ∠P and ∠Q. Line LOM is drawn parallel to PQ. Prove that :
(i) PL = QM (ii) LO = OM.
Solution: Since PQRS is a parallelogram.
∴ PS || QR ⇒ PL || QM
Thus, we have
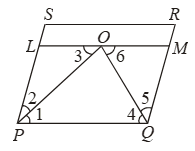
PL || QM and LM || PQ [Given]
⇒ PQML is parallelogram.
⇒ PL = QM [∵ Opp. sides of a || gm are equal]
This proves (i).
Now, OP is the bisector of ∠P
∴ ∠1 = ∠2 ….(i)
Now, PQ || LM and transversal OP intersects them
∴ ∠1 = ∠3 ….(ii)
From (i) and (ii), we get ∠2 = ∠3
Thus, in ∆OPL, we have
∠2 = ∠3
⇒ OL = PL …(iii)
[∵ Opp. sides of equal angles are equal]
Since OQ is the bisector of ∠Q
∴ ∠4 = ∠5 ….(iv)
Also, PQ || LM and transversal OQ intersects them
∠4 = ∠6 ….(v)
From (iv) and (v), we get
∠5 = ∠6
Thus, in ∆OQM, we have
∠5 = ∠6
⇒ OM = QM ….(vi)
[∵ Opp. sides of equal angles are equal]
But, PL = QM ….(vii) [As proved above]
So, from (iii), (vi) and (vii), we get
OL = OM.
Example 22: The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
Solution: Given: A quadrilateral whose diagonals AC and BD are perpendicular to each other, P, Q, R, S are the mid-points of sides AB, BC, CD and DA respectively. PQ, QR, RS and SP are joined.
To Prove: PQRS is a rectangle.
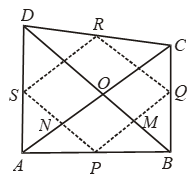
Proof: In ∆ABC, P and Q are the mid-points of AB and BC respectively.
∴ PQ || AC and PQ = 1/2 AC …. (i)
In ∆ADC, R and S are the mid-points of CD and AD respectively.
∴ RS || AC and RS = 1/2 AC ….(ii)
From (i) and (ii), we have
PQ || RS and PQ = RS
Thus, in quadrilateral PQRS, a pair of opposite sides are equal and parallel. So, PQRS is a parallelogram.
Suppose the diagonals AC and BD of quadrilateral ABCD intersect at O.
Now in ∆ABD, P is the mid-point of AB and S is the mid-point of AD.
∴ PS || BD ⇒PN || MO
Also, from (i) , PQ || AC
⇒ PM || NO
Thus, in quadrilateral PMON, we have
PN || MO and PM || NO
⇒ PMON is a parallelogram.
⇒ ∠MPN = ∠MON
[∵ Opposite angles of a parallelogram are equal]
⇒ ∠MPN = ∠BOA [∵ ∠BOA = ∠MON]
⇒ ∠MPN = 90º [∵ AC ⊥ BD ∴ ∠BOA = 90º]
⇒ ∠QPS = 90º [∵ ∠MPN = ∠QPS]
Thus, PQRS is a parallelogram whose one angle ∠QPS = 90º Hence PQRS is a rectangle.
Example 23: In a parallelogram ABCD diagonals AC and BD intersect at O and AC = 6.8cm and
BD = 13.6 cm. Find the measures of OC
and CD.
Solution: Since the diagonals of a parallelogram bisect each other. Therefore, O is the mid-point of AC and BD.
∴ OC = 1/2 AC = 1/2 × 6.8 cm = 3.4 cm
and, OD = 1/2 BD = 1/2 × 5.6 cm = 2.8 cm
Example 24: Prove that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
Solution: Given: ABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively.
To Prove: PQRS is a parallelogram.
Construction: Join A and C.
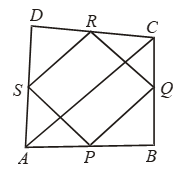
Proof: In ∆ABC, P and Q are the mid-points of sides AB and BC respectively.
∴ PQ || AC and PQ = 1/2 AC …. (i)
In ∆ADC, R and S are the mid-points of CD and AD respectively.
∴ RS || AC and RS = 1/2 AC ….(ii)
From (i) and (ii), we have
PQ = RS and PQ || RS
Thus, in quadrilateral PQRS one pair of opposite sides are equal and parallel.
Hence, PQRS is a parallelogram.
Example 25: The side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CF meets CB produced in Q and the parallelogram PBQR completed.
Show that ar (parallelogram ABCD) = ar (parallelogram BPRQ).
Solution: Construction: Join AC and PQ.
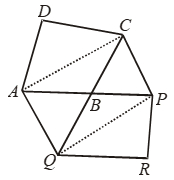
To prove: ar (parallelogram ABCD) = ar(parallelogram BPRQ)
Proof: Since AC and PQ are diagonals of parallelograms ABCD and BPQR respectively.
∴ ar (∆ABC) = 1/2 ar (parallelogram ABCD) ….(i)
and, ar (∆PBQ) = 1/2 ar (parallelogram BPRQ) ….(ii)
Now, ∆s ACQ and AQP are on the same base AQ and between the same parallels AQ and CP
∴ ar(∆ACQ) = ar (∆AQP)
⇒ ar(∆ACQ) – ar (∆ABQ)
= ar (∆AQP)–ar(∆ABQ)
[Subtracting ar (∆ABQ) from both sides]
⇒ ar (∆ABC) = ar (∆BPQ)
⇒ 1/2 ar (parallelogram ABCD ) = 1/2 ar (parallelogram BPRQ)
[Using (i) and (ii)]
⇒ ar(parallelogram ABCD) = ar(parallelogram BPRQ).
Example 26: In a parallelogram ABCD, the bisector of ∠A also bisects BC at X. Prove that AD = 2AB.
Solution: Since AX is the bisector of ∠A.
∴ ∠1 = 1/2 ∠A …. (i)
Since ABCD is a parallelogram.
Therefore, AD || BC and AB intersects them.
⇒ ∠A + ∠B = 180º
[∵ Sum of interior angles is 180º]
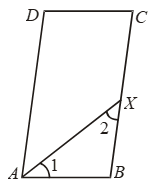
⇒ ∠B = 180º – ∠A
In ∆ABX, we have
∠1 + ∠2 + ∠B = 180º
⇒ 1/2 ∠A + ∠2 + 180º – ∠A = 180º
⇒ ∠2 – 1/2 ∠A = 0
⇒ ∠2 = 1/2 ∠A ….(ii)
From (i) and (ii), we have ∠1 = ∠2.
Thus, in ∆ABX, we have
∠1 = ∠2.
⇒ BX = AB [∵ Sides opposite to equal angles in a ∆ are equal]
⇒ 2BX = 2AB [Multiplying both sides by 2]
⇒ BC = 2AB [∵ X is the mid-point of BC
∴ AD = BC]
⇒ AD = 2AB
[∵ ABCD is a parallelogram ∴ AD = BC]
Example 27: In Fig. BC || XY, BX || CA and AB || YC. Prove that:
ar (∆ABX) = ar (∆ACY).
Solution: Join XC and BY.
Since ∆s BXC and BCY are on the same base BC and between the sum parallels BC and XY
∴ ar(∆BXC) = ar(∆BCY) …. (i)
Also, ∆s BXC and ABX are on the same base BX and between the same parallels BX and AC.
∴ ar (∆BXC) = ar (∆ABX) ….(ii)
Clearly, ∆sBCY and ACY are on the same base CY and between the same parallels
AB and CY.
∴ ar(∆BCY) = ar (∆ACY) ….(iii)
From (i), (ii) and (iii), we get
ar(∆ABX) = ar (∆ACY).
Example 28: In Fig. AD and BE are medians of ∆ABC and BE || DF.
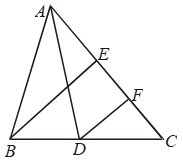
Prove that CF = 1/4 AC
Solution: In ∆BEC, DF is a line through the mid-point D of BC and parallel to BE intersecting CE at F. Therefore, F is the mid-point of CE. Because the line drawn through the mid-point of one side of a triangle and parallel to another side bisects the third side.
Now, F is the mid-point of CE
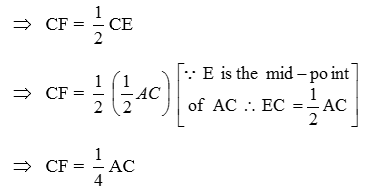
Example 29: D, E, F are the mid-points of the sides BC, CA and AB respectively of ∆ABC, prove that BDEF is a parallelogram whose area is half that of ∆ABC. Also, show that
ar (∆DEF) = 1/4 are (∆ABC).
Solution: Since D and E are the mid-points of sides BC and AC respectively.
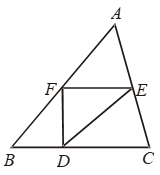
Therefore, DE || BA ⇒ DE || BF
Similarly, FE || BD. So, BDEF is a parallelogram.
Similarly, DCEF and AFDE are parallelograms.
Now, DF is a diagonal of parallelogram BDEF.
∴ ar (∆BDF) = ar (∆DEF) …. (i)
DE is a diagonal of parallelogram DCEF
∴ ar (∆DCE) = ar (∆DEF) ….(ii)
FE is a diagonal of parallelogram AFDE
∴ ar (∆AFE) = ar (∆DEF) ….(iii)

Example 30: ∆ABC and ∆DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF; show that AC is equal and parallel to DF.
Solution: Given:Two triangles ABC and DEF such that
AB = DE and AB || DE. Also BC = EF and BC || EF
To Prove: AC = DF and AC || DF
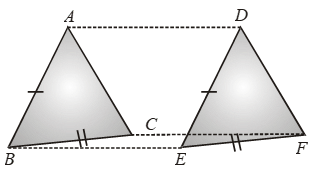
Proof: Consider the quadrilateral ABED.
We have, AB = DE and AB || DE
⇒ One pair of opposite sides are equal and parallel
⇒ ABED is a parallelogram.
⇒ AD = BE and AD || BE ….(i)
Now, consider quadrilateral BCFE.
We have, BC = EF and BC || EF
⇒ One pair of opposite sides are equal and parallel
⇒ BCFE is a parallelogram.
⇒ CF = BE and CF || BE ….(ii)
From (i) and (ii), we have
AD = CF and AD || CF
⇒ ACFD is a parallelogram
AC = DF and AC || DF
Example 31: Parallelogram ABCD & rectangle ABEF have the same base AB and also have equal areas. Show that perimeter of the parallelogram is greater than that of the rectangle.
Solution: Given: A parallelogram ABCD and a rectangle ABEF with the same base AB and equal areas.
To Prove: Perimeter of parallelogram ABCD > Perimeter of rectangle ABEF
i.e. AB + BC + CD + AD > AB + BE + EF + AF.
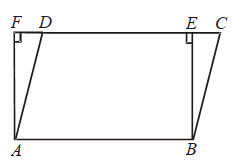
Proof: Since opposite sides of a parallelogram and a rectangle are equal.
∴ AB = DC [∵ ABCD is a parallelogram]
and, AB = EF [∵ ABEF is a rectangle]
∴ DC = EF …. (i)
⇒ AB + DC = AB + EF ….(ii)
Since, of all the segments that can be drawn to a given line from a point not lying on it, the perpendicular segment is the shortest.
∴ BE < BC and AF < AD ⇒ BC > BE and AD > AF
⇒ BC + AD > BE + AF ….(iii)
Adding (ii) and (iii), we get
AB + DC + BC + AD > AB + EF + BE + AF
⇒ AB + BC + CD + DA > AB + BE + EF + FA.
Example 32: In ∆ABC, AD is the median through A and E is the mid-point of AD. BE produced meets AC in F. Prove that AF = 1/3 AC.
Solution: Through D, draw DK || BF. In ∆ADK, E is the mid-point of AD and EF || DK.
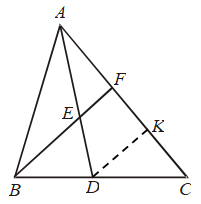
∴ F is the mid-point of AK
⇒ AF = FK …. (i)
In ∆BCF, D is the mid-point of BC and
DK || BF
∴ K is the mid-point of FC
∴ FK = KC ….(ii)
From (i) and (ii), we have
AF = FK = KC ….(iii)
Now, AC = AF + FK + KC
⇒ AC = AF + AF + AF [Using (iii)]
⇒ AC = 3 (AF)
⇒ AF = 1/3 AC