How To Find The Area Of A Sector Of A Circle

How To Find The Area Of A Sector Of A Circle

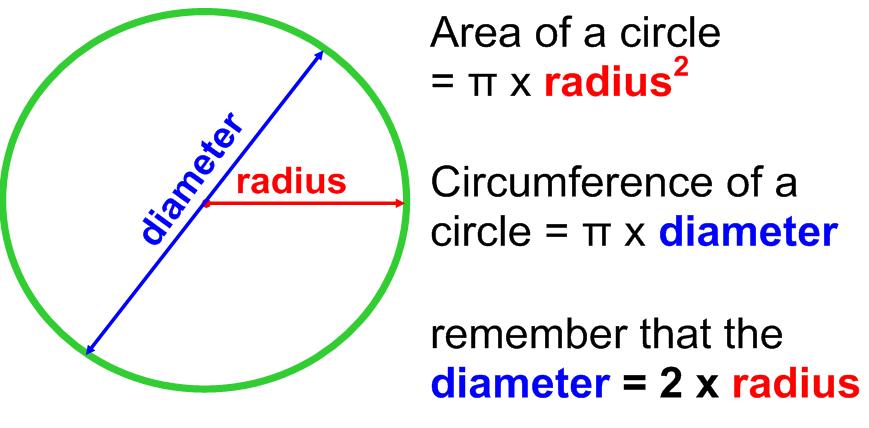
If the arc subtends an angle of θ at the centre, then its arc length is
\( \frac{\text{ }\!\!\theta\!\!\text{ }}{\text{180}}\text{ }\!\!\times\!\!\text{ }\!\!\pi\!\!\text{ r} \)
Hence, the arc length ‘l’ of a sector of angle θ in a
circle of radius r is given by
\( l=\frac{\text{ }\!\!\theta\!\!\text{ }}{\text{180}}\text{ }\!\!\times\!\!\text{ }\!\!\pi\!\!\text{ r }…….\text{ (i)} \)
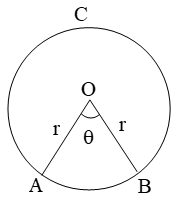
If the arc subtends an angle θ, then area of the corresponding sector is
\( \frac{\pi {{r}^{2}}\theta }{360} \)
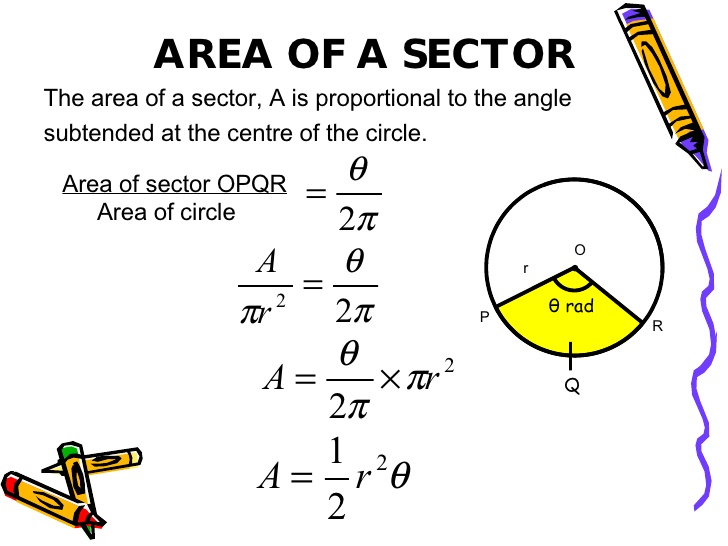
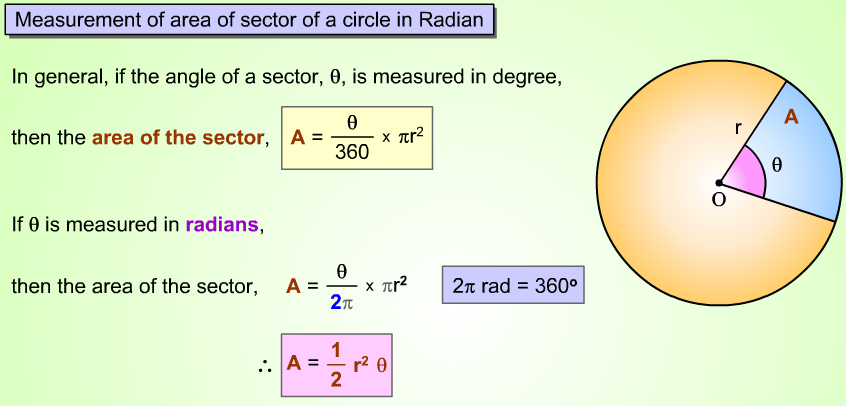
Thus, the area A of a sector of angle θ in a circle of radius r is given by
\( A=~\frac{\theta }{360}\text{ }\times \text{ }\!\!\pi\!\!\text{ }{{r}^{2}} \)
\( =\frac{\theta }{360}\text{ }\times \text{ }\left( \text{Area of the circle} \right)\text{ }……..\text{ (ii)} \)
= × (Area of the circle) ….(ii)
Some useful results to remember:
(i) Angle described by minute hand in 60 minutes = 360º
Angle described by minute hand in one minute
\( ={{\left( \frac{360}{60} \right)}^{0}}=\text{ }6{}^\text{o} \)
Thus, minute hand rotates through an angle of 6º in one minute.
(ii) Angle described by hour hand in 12 hours = 360º
Angle described by hour hand in one hour
\( =\left( \frac{360}{12} \right)_{{}}^{0}=30{}^\text{o} \)

Read More:

• Parts of a Circle
• Perimeter of A Circle
• Common Chord of Two Intersecting Circles
• Construction of a Circle
• The Area of A Circle
• Properties of Circles
• Sector of A Circle
• The Area of A Segment of A Circle

Area Of A Sector Of A Circle With Examples

Example 1:    A sector is cut from a circle of radius 21 cm. The angle of the sector is 150º. Find the length of its arc and area.
Sol.    The arc length l and area A of a sector of angle θ in a circle of radius r are given by
\( l=\frac{\theta }{360}\times 2\pi r\text{  and  A=}\frac{\theta }{360}\times \pi {{r}^{2}}\text{ respectively}\text{.} \)
Here, r = 21 cm and q = 150
\(\text{ }l=\left\{ \frac{150}{360}\times 2\times \frac{22}{7}\times 21 \right\}\text{cm}=\text{55 cm} \)
\( \text{and A}=\left\{ \frac{150}{360}\times \frac{22}{7}\times {{(21)}^{2}} \right\}c{{m}^{2}}=\frac{1155}{2}c{{m}^{2}} \)
= 577.5 cm²

Example 2:    Find the area of the sector of a circle whose radius is 14 cm and angle of sector is 45º.
Sol.    We know that the area A of a sector of angle θ in a circle of radius r is given by
\( A=\frac{\theta }{360}\text{ }\times \text{ }\pi {{r}^{2}} \)
Here, r = 14 cm and θ = 45
\(A=\left\{ \frac{45}{360}\times \frac{22}{7}\times {{(14)}^{2}} \right\}c{{m}^{2}}\)
\( =\left\{ \frac{1}{8}\times \frac{22}{7}\times 14\times 14 \right\}c{{m}^{2}} \)
= 77 cm²

Example 3:    In Fig. there are shown sectors of two concentric circles of radii 7 cm and 3.5 cm. Find the area of the shaded region. (Use π = \(\frac { 22 }{ 7 }\)).
Sol.    Let A₁ and A₂ be the areas of sectors OAB and OCD respectively. Then, A₁ = Area of a sector of angle 30º in a circle of radius 7 cm

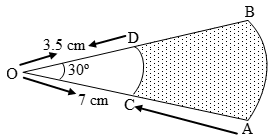
\( {{A}_{1}}=\left\{ \frac{30}{360}\times \frac{22}{7}\times {{7}^{2}} \right\}c{{m}^{2}}\text{ }\left[ U\sin g:A=\frac{\theta }{360}\times \pi {{r}^{2}}\, \right] \)
⇒ A₁ = \(\frac { 77 }{ 6 }\) cm²
A₂ = Area of a sector of angle 30º in a circle of radius 3.5 cm.
∴  Area of the shaded region
\({{A}_{2}}=\left\{ \frac{30}{360}\times \frac{22}{7}\times {{(3.5)}^{2}} \right\}c{{m}^{2}} \)
\({{A}_{2}}=\left\{ \frac{1}{12}\times \frac{22}{7}\times \frac{7}{2}\times \frac{7}{2} \right\}c{{m}^{2}}=\frac{77}{24}c{{m}^{2}} \)
\( ={{A}_{1}}-{{A}_{2}}=\left( \frac{77}{6}-\frac{77}{24} \right) \)
= \(\frac { 77 }{ 24 }\) × (4 – 1) cm² = \(\frac { 77 }{ 8 }\) cm² = 9.625 cm²

Example 4:    A pendulum swings through an angle of 30º and describes an arc 8.8 cm in length. Find the length of the pendulum.
Sol.      Here, q = 30º, l = arc = 8.8 cm
\( l=\frac{\theta }{360}\times 2\pi r \)
\( 8.8=~\frac{30}{360}\times 2\times \frac{22}{7}\times r~ \)
\( r=\frac{8.8\times 6\times 7}{22}=16.8\text{ }cm \)

Example 5:    The length of minute hand of a clock is 14 cm. Find the area swept by the minute hand in one minute. (Use π = 22/7)
Sol.     Clearly, minute hand of a clock describes a circle of radius equal to its length i.e., 14 cm.
Since the minute hand rotates through 6º in one minute. Therefore, area swept by the minute hand in one minute is the area of a sector of angle 6º in a circle of radius 14 cm. Hence, required area A is given by
\( A=\frac{\theta }{360}\times \pi {{r}^{2}}~ \)
\( A=\left\{ \frac{6}{360}\times \frac{22}{7}\times {{(14)}^{2}} \right\} \)
\( A=\left\{ \frac{1}{60}\times \frac{22}{7}\times 14\times 14 \right\}=\frac{154}{15} \)
= 10.26 cm²

Example 6:    The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
Sol.    Let OAB be the given sector. Then,
Perimeter of sector OAB = 16.4 cm

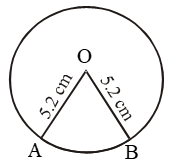
⇒ OA + OB + arc AB = 16.4 cm
⇒ 5.2 + 5.2 + arc AB = 16.4
⇒ arc AB = 6 cm
⇒ l = 6 cm
∴ Area of  sector OAB = \(\frac { 1 }{ 2 }\) lr
= \(\frac { 1 }{ 2 }\) × 6 × 5.2 cm² = 15.6 cm²

Example 7:    The minute hand of a clock is 10cm long. Find the area of the face of the clock described by the minute hand between 9 A.M. and 9.35 A.M.
Sol.    We have,
Angle described by the minute hand in one minute = 6º
∴ Angle described by the minute hand in
35 minutes = (6 × 35)º = 210º
∴ Area swept by the minute hand in 35 minutes
= Area of a sector of angle 210º in a circle of radius 10 cm
\(=\left\{ \frac{210}{360}\times \frac{22}{7}\times {{(10)}^{2}} \right\}c{{m}^{2~}}=\text{ }183.3\text{ }c{{m}^{2}}~\text{             }\left[ \text{Using  }A=\frac{\theta }{360{}^\text{o}}\times \pi {{r}^{2}} \right] \)

Example 8:    The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days.
(Take π = 22/7)
Sol.    In 2 days, the short hand will complete 4 rounds.
∴ Distance moved by its tip = 4 (Circumference of a circle of radius 4 cm)
\( =4\times \left( 2\times \frac{22}{7}\times 4 \right)=\frac{704}{7}\text{ cm} \)
In 2 days, the long hand will complete 48 rounds.
∴ Distance moved by its tip
= 48 (Circumference of a circle of radius 6 cm)
\( =48\times \left( 2\times \frac{22}{7}\times 4 \right)=\frac{12672}{7}\text{ cm} \)
Hence,
Sum of the distance moved by the tips of two hands of the clock
\( =\left( \frac{704}{7}+\frac{12672}{7} \right)=\text{ }1910.57\text{ }cm \)

Example 9:    An elastic belt is placed round the rim of a pulley of radius 5 cm. One point on the belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from O. Find the length of the belt that is in contact with the rim of the pulley. Also, find the shaded area.
Sol.    In the adjacent figure, let ∠AOP = ∠BOP = θ. Clearly, portion AB of the belt is not in contact with the rim of the pulley. In right triangle OAP, we have

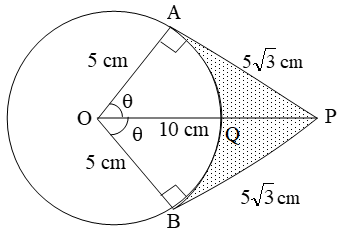
\( \cos \theta =\frac{OA}{OP}=\frac{5}{10}=\frac{1}{2}\text{ }\Rightarrow \text{ }\theta =\text{ }60{}^\text{o} \)
⇒ ∠AOB = 2θ = 120º
\(\text{Arc AB}=\frac{120{}^\text{o}\times 2\times \pi \times 5}{360}=\frac{10\pi }{3}cm \)
\( \left[ \text{Using }l=\frac{\theta }{360}\times 2\pi r \right] \)
Hence, Length of the belt that is in contact with the rim of the pulley
= Circumference of the rim – Length of arc AB
\( =\text{ }2\pi \times 5-\frac{10\pi }{3}=\frac{20\pi }{3}~cm \)
Now,
Area of sector OAQB = \(\frac { 1 }{ 2 }\) × π × 5² cm²
\( =\frac{25\pi }{3}\text{ c}{{\text{m}}^{2}}\text{   }\left[ \text{Using}Area=\frac{\theta }{360}\times \pi {{r}^{2}} \right] \)
Area of quadrilateral OAPB = 2 (Area of ∆OAP)
= 2 × (1/2 × OA × AP)
= 5 × 5√3 cm²
[∵ OP² = OA² + AP²   ⇒  AP = \(\sqrt{100-25}\) = 5√3 ]
= 25√3 cm²
Hence,
Shaded area = Area of quadrilateral
OAPB – Area of sector OAQB.
\( =\left( 25\sqrt{3}-\frac{25\pi }{3} \right)=\frac{25}{3}(3\sqrt{3}-\pi )\text{ c}{{\text{m}}^{\text{2}}} \)

Example 10:    An arc of a circle is of length 5π cm and the sector it bounds has an area of 20 π cm². Find the radius of the circle.
Sol.    Let the radius of the circle be r cm and the arc AB of length 5π cm subtends angle θ at the centre O of the circle. Then,
Arc AB = 5π cm and
Area of sector OAB = 20π cm²

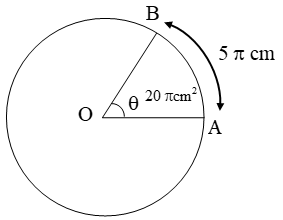
\( \Rightarrow \frac{\theta }{360}\times 2\pi r=5\pi \text{ and }\frac{\theta }{360}\times \pi {{r}^{2}}=20\pi \)
\( \Rightarrow \frac{\frac{\theta }{360}\times \pi {{r}^{2}}}{\frac{\theta }{360}\times 2\pi r}=\frac{20\pi }{5\pi } \)
⇒ r/2 = 4  ⇒   r = 8 cm
ALTER: We have, Area = 1/2 l r ⇒20π
= 1/2 × 5π × r = 8 cm

Example 11:    An umbrella has 8 ribs which are equally spaced. Assuming umbrella to be a flat circle of radius 45 cm. Find the area between the two consecutive ribs of the umbrella.
Sol.    Since ribs are equally spaced. Therefore,
Angle made by two consecutive ribs at the centre = \(\frac { 360 }{ 8 }\) = 45º

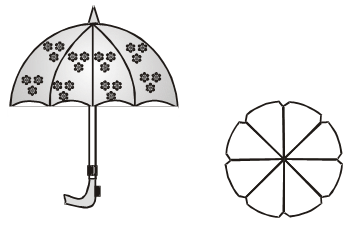
Thus,
Area between two consecutive ribs
= Area of a sector of a circle of radius 45 cm and sector angle 45º
\(=\left\{ \frac{45}{360}\times \frac{22}{7}\times 45\times 45 \right\}\text{c}{{\text{m}}^{2}}\text{ }\left[ \text{Using }Area=\frac{\theta }{360}\times \pi {{r}^{2}} \right] \)
=  \(\frac { 1 }{ 8 }\) × \(\frac { 22 }{ 7 }\) × 45× 45 cm² = 795.53 cm²

Example 12:    A brooch is made with silver wire in the form of a circle with diameter 35 mm. The wire also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. Find:
(i) the total length of the silver wire required
(ii) the area of each sector of the brooch.
Sol.    (i) We have,

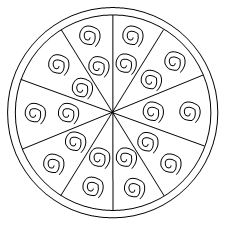
Total length of the silver wire = Circumference of the circle of radius
35/2 mm + Length of five diameters
= 2π × \(\frac { 35 }{ 2 }\) + 5 × 35 mm
\( =\left( 2\times \frac{22}{7}\times \frac{35}{2}+175 \right)\text{ mm} \)
= 285 mm
(ii)  The circle is divided into 10 equal sectors, Therefore, Area of each sector of the brooch
= 1/10 (Area of the circle)
= 1/10 × π  × (35/2)² cm²
\( \text{=}\frac{1}{10}\times \frac{22}{7}\times \frac{35}{2}\times \frac{35}{2}\text{ m}{{\text{m}}^{2}} \)
\( =\frac{385}{4}\text{ m}{{\text{m}}^{2}} \)